Физическото значение на FFT

За какво е бързото преобразуване на Фурие или дискретно преобразуване на Фурие (DFT)? Нека се опитаме да го разберем.

Да предположим, че имаме синусова функция x = sin (t).

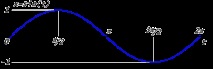
Максималната амплитуда на това трептене е 1. Ако го умножим по някакъв коефициент А, ще получим същата графика, опъната вертикално по А пъти: x = Asin (t).

Периодът на трептене е 2π. Ако искаме да увеличим периода до T, тогава трябва да умножим променливата t по коефициент. Това ще разтегне графиката хоризонтално: x = A sin (2πt/T).

Честотата на трептенията е противоположна на периода: ν = 1/T. Те говорят и за кръговата честота, която се изчислява по формулата: ω = 2πν = 2πT. Откъде: x = Грех (ωt).

И накрая, има фаза, наречена φ. Той определя изместването на графика на флуктуацията наляво. Комбинацията от всички тези параметри води до хармонично трептене или просто хармоничен:

Изразът на хармоника от гледна точка на косинуса изглежда много подобен:

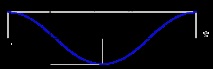
Няма голяма разлика. Достатъчно е да промените фазата с π/2, за да преминете от синус в косинус и обратно. По-нататък имаме предвид под хармоника косинусовата функция:

x = A cos (2πt/T + φ) = A cos (2πνt + φ) = A cos (ωt + φ) (1)

В природата и технологиите вибрациите, описани от такава функция, са изключително често срещани. Например махало, струна, водни и звукови вълни и др. И т.н.

Преобразуваме (1) по формулата за косинуса на сумата:

x = A cos φ cos (2πt/T) - A sin φ sin (2πt/T) (2)

Нека да изберем елементи в (2), които са независими от t, и да ги обозначим като Re и Im:

x = Re cos (2πt/T) - Im sin (2πt/T) (3)
Re = A cos φ, Im = A sin φ

Стойностите на Re и Im могат да се използват за еднозначно възстановяване на амплитудата и фазата на оригиналната хармоника:

и (4)

Сега нека вземем обратното преобразуване на Фурие:

(пет)

Нека извършим следните действия върху тази формула: разлагаме всеки комплекс Xk на въображаеми и реални компоненти Xk = Rek + j Imk; декомпозира степента по формулата на Ойлер в синуса и косинуса на реалния аргумент; умножете; добавете 1/N под знака за сумата и пренаредете елементите в две суми:

(6)

Нека оставим тази формула настрана засега и да разгледаме една много често срещана ситуация. Нека имаме звук или някаква друга вибрация под формата на функция x = f (t). Нека това колебание да бъде записано под формата на графика за интервала от време [0, T]. За обработка от компютър трябва да изпълните вземане на проби. Сегментът е разделен на N-1 части и стойностите на функцията x0, x1, x2 се запазват. xN за N точки на границите на сегментите t0 = 0, t1 = T/N, t2 = 2T/N. tn = nT/N. tN = T.

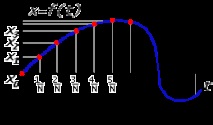
В резултат на директното дискретно преобразуване на Фурие са получени N стойности за Xk:

(7)

Сега, ако приложим обратното дискретно преобразуване на Фурие, ще получим оригиналната последователност. Оригиналната последователност се състои от реални числа и последователността обикновено е сложна. Сега да се върнем към формула (6). Вляво има реално число xn, а вдясно има две суми, едната от които се умножава по въображаемата единица j. Самите суми се състоят от реални условия. От това следва, че втората сума е нула, ако първоначалната последователност е била валидна. Нека го пуснем и да получим:

(8)

Тъй като по време на дискретизацията взехме tn = nT/N и xn = f (tn), можем да извършим заместването: n = tnN/T. Следователно, в синус и косинус, вместо 2πkn/N, можете да напишете 2πktn/T. В резултат получаваме:

(девет)

Нека сравним тази формула с формули (1) и (3) за хармоника:

x = A cos (2πt/T + φ) = A cos (2πνt + φ) = A cos (ωt + φ) (1)
x = Re cos (2πt/T) - Im sin (2πt/T) (3)

Виждаме, че сумата (9) е сумата от N хармонични трептения на различни честоти, фази и амплитуди:

(десет)

По-долу ще използваме функцията

обадете се k-та хармоника.

Амплитудата, фазата, честотата и периодът на всяка от хармониците са свързани с коефициентите Xk по формулите:

(12)

Физическият смисъл на дискретното преобразуване на Фурие е да представлява някакъв дискретен сигнал като сбор от хармоници. Параметрите на всяка хармоника се изчисляват чрез директно преобразуване, а сумата на хармониците - чрез обратно.