Хамилтонови графики

Целта на курсовата ми работа е:

1. Запознаване с основните понятия, свързани с хамилтоновите графики и цикли.

2. Разгледайте проблемите и методите за намиране на хамилтонови цикли в графики

3. Създаване на програма за намиране на хамилтонови цикли.

На първо място, за да се изясни и изясни терминологията, бих искал да дам определения на някои елементи на графиката, като маршрут, верига, цикъл.

По маршрут в графиката G(V, E) се нарича редуваща се последователност от върхове и ребра:, ..., в която всеки два съседни елемента са инцидентни. Ако =, тогава маршрутът е затворен, в противен случай е отворен.

Ако всички ръбове са различни, тогава маршрутът се нарича верига. Ако всички върхове (а оттам и ръбовете) са различни, тогава маршрутът се нарича проста верига.

Затворена верига се нарича цикъл; затворена проста верига се нарича прост цикъл. Графика без цикли се нарича ациклична. За диграфите веригата се нарича път, а цикълът се нарича контур.

Основни определения и резултати

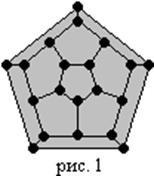
Името "хамилтонов цикъл" идва от проблема "Пътуване около света", предложен от ирландския математик Уилям Хамилтън през 1859 година. След напускането на първоначалния връх на графиката беше необходимо да се обиколят всичките й върхове и да се върне към началната точка. Графиката представлява подреждане на додекаедър, на всеки от 20-те върха на графиката е присвоено името на голям град в света.

Ако графиката има прост цикъл, съдържащ едновременно всички върхове на графиката, тогава се нарича такъв цикъл Хамилтонов цикъл, и графиката се извиква Хамилтонова графика. Извиква се графика, която съдържа прост път през всеки от нейните върхове полухамилтонов. Тази дефиниция може да бъде разширена до насочени графики, ако пътят се счита за насочен.

Хамилтоновият цикъл не включва непременно всички ръбове на графиката. Ясно е, че само свързан граф може да бъде хамилтонов и че всеки хамилтонов граф е полухамилтонов. Имайте предвид, че хамилтоновият цикъл не съществува във всяка графика.

Коментирайте.

Всеки брой G може да се превърне в хамилтонов граф чрез добавяне на достатъчен брой върхове. За това например е достатъчно до върховете v1, ..., vp броя G добавяне на върхове u1, ..., нагоре и множеството от ръбове vi, ui)> ui, vi + 1)>.

Степента на връх v е броят на ребрата д(v) инцидент с него и цикълът се брои два пъти. В случай на насочена графика степента направете(v) по изходящите дъги и ди(v) - чрез входящи.

За разлика от графовете на Ойлер, където има критерий графът да бъде Ойлер, за хамилтоновите графики няма такъв критерий. Освен това проблемът с проверката на съществуването на хамилтонов цикъл се оказва NP-пълен. Повечето от известните теореми са от вида: „ако графиката G има достатъчен брой ребра, тогава графиката е хамилтонова. " Даваме няколко такива теореми.

Теореми за достатъчност за хамилтонов граф

Теорема (Dirac, 1952) 1. Ако в проста графика с н ? 3 върха стр(v) ? н/ 2 за всеки връх v, след това графиката G е Хамилтонов.

Коментирайте Има няколко доказателства за тази добре позната теорема, тук даваме доказателство от Д. Дж. Нюман.

Доказателства. Добавете към нашата графика к нови върхове, свързващи всеки от тях с всеки връх от G. Ще приемем това к -- най-малкият брой върхове, необходими за получената графика Gстана хамилтонов. След това, като се има предвид това к > 0, стигаме до противоречие.

Нека бъде v>стр>w> ...>v Хамилтонов цикъл в графика G, Където v, w-- върхове от G, и стр-- един от новите върхове. Тогава w не е в съседство с v, тъй като в противен случай може да не използваме върха стр, което противоречи на минималността к. Освен това, отгоре, да речем, w, съседен връх w, не може директно да следва върха v, съседен връх v, защото тогава бихме могли да заменим v>стр>w> ...>v> w>v На v>v> ...>w>w> ...>v, обръщайки частта от цикъла между w и v. Оттук следва, че броят на върховете на графиката G, не е съседно на w, поне броя на върховете, съседни на v (т.е. равно на поне, н/ 2 + к); от друга страна, очевидно е, че броят на върховете на графиката G, съседен на w, също е равно поне, н/ 2 + к. И тъй като няма връх на графиката Gне може да бъде както съседен, така и несъседен връх w, тогава общият брой на върховете на графиката G, равен н + к, не по-малко от н + 2к. Това е желаното противоречие.

Теорема (руда) 2. Ако броят на върховете на графиката G(V, E) н ? 3 и за всеки два несъседни върха u и v важи неравенството:

Графика G има хамилтонов цикъл, ако е изпълнено едно от следните условия:

Състояние на Бонди: от d (vi)? i и d (vk)? k => d (vi) + d (vk)? n (k? i)

Грабвано състояние: на д(vk) ? к? n/2 => d(vn-k) ? n k.

Освен това е известно, че почти всички графики са хамилтонови, т.е.

Където З.(стр) е множеството на хамилтоновите графики с стр върхове и G(стр) е множеството от всички графики с p върхове. Проблемът за намирането на хамилтонов цикъл или еквивалентния проблем на пътуващия продавач е практически търсен, но за него не е известен (и най-вероятно не съществува) ефективен алгоритъм за решаване.

Пример граф, когато условието на теоремата на Дирак не е изпълнено, но графиката е хамилтонова.

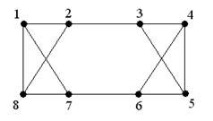
н = 8; д(vi) = 3; 3? 8/2 = 4 не е хамилтонов граф, но има хамилтонов цикъл: М = (1, 2, 3, 4, 5, 6, 7, 8, 1)