Методът на четиримата руснаци за матрично умножение

Ако разгледаме произведението на матрици [math] C = A \ cdot B [/ math] по дефиниция [math] \ left (c_ = \ sum \ limit_ ^ n a_b_ \ right) [/ math], тогава сложността на алгоритъмът ще бъде [math] O (n ^ 3) [/ math] - всеки от [math] n ^ 2 [/ math] елементите на получената матрица [math] C [/ math] се изчислява във време, пропорционално на [ математика] n [/ математика] .

Сега ще бъде показано как леко да намалим това време.

За да извършим компресиране на матрици, извършваме следното предварително изчисление: за всички възможни двойки двоични вектори с дължина [math] k [/ math], изчисляваме и съхраняваме техния скаларен продукт по модул [math] 2 [/ math] .

Да вземем първата матрица. разделете всяка от линиите му на парчета с размер [math] k [/ math]. За всяка фигура определяме номера на двоичния вектор, който съответства на числата на тази фигура. Ако парчето е неравномерно по дължина [math] k [/ math] (последното парче от реда), тогава ще приемем, че в края съдържа нули, които не влияят на умножението. Получаваме матрицата [math] A'_ \ rceil> [/ math] .

Нека направим същото с матрицата [math] B [/ math], разделяйки колони вместо редове. Получаваме матрицата [math] B '_ [/ math] .

Сега, ако вместо произведението на матриците [math] A [/ math] и [math] B [/ math], ние разглеждаме произведението на новите матрици [math] A '[/ math] и [math] B '[/ math], използвайки изчислените скаларни продукти, тогава всеки елемент от матрицата [math] C [/ math] ще бъде получен вече във време, пропорционално на [math] \ lceil \ dfrac \ rceil [/ math] вместо [ math] n [/ math], а времето на матричния продукт ще бъде намалено от [math] O (n ^ 3) [/ math] на [math] O (n ^ 2 \ cdot \ dfrac nk) = O (\ dfrac) [/ математика] .

Нека да оценим асимптотиката на този алгоритъм.

Предварителното изчисление на точки работи в [math] O (2 ^ k) [/ math] .
Създаване на матрици [math] A '[/ math] и [math] B' [/ math] - [math] O (n ^ 2) [/ math] .
Умножение на получените матрици - [math] O (\ dfrac) [/ math] .

Общо: [математика] O (2 ^ k) + O (\ dfrac) [/ математика]. Избирайки [math] k = \ log n [/ math], получаваме необходимата асимптотика [math] O (n ^ 2 \ log n) + O (\ dfrac) = O (\ dfrac) [/ math]

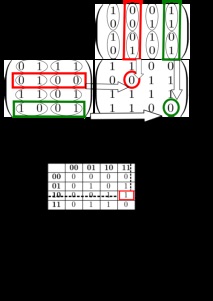
Нека разгледаме работата на алгоритъма на примера на умножаване на две матрици [math] A [/ math] и [math] B [/ math], където

[math] A = [/ math] [math] \ left (\ begin 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \ край \ вдясно) [/ math], [math] B = [/ math] [math] \ left (\ begin 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \ край \ вдясно) [/ math]

[math] k = \ log_2 n = \ log_2 4 = 2 [/ math], след това изчисляваме предварително всички скаларни продукти:

За удобство всеки битов вектор ще съответства на двоично число с водещи нули, т.е. в този случай имаме числа [math] 00 [/ math], [math] 01 [/ math], [math] 10 [/ math], [math] 11 [/ math]. По-долу има таблица, в която са записани всички търсени произведения:

[math] \ begin \ hline & \ textbf & \ textbf & \ textbf & \ textbf \\ \ hline \ textbf & 0 & 0 & 0 & 0 \\ \ hline \ textbf & 0 & 1 & 0 & 1 \\ \ hline \ textbf & 0 & 0 & 1 & 1 \\ \ hline \ textbf & 0 & 1 & 1 & 0 \\ \ hline \ end [/ math]

По конвенция относно битовите вектори и двоичните числа получаваме нови матрици [math] A '[/ math] и [math] B' [/ math]:

[math] A '= [/ math] [math] \ left (\ begin 01 & 11 \\ 01 & 00 \\ 11 & 01 \\ 10 & 01 \ end \ right) [/ math], [math] B '= [/ math] [math] \ left (\ begin 10 & 00 & 01 & 11 \\ 10 & 01 & 10 & 01 \ end \ right) [/ math]

Нека умножим тези матрици по модул две, като използваме нашето предварително разглеждане:

[math] C = A '\ times B' = [/ math] [math] \ left (\ begin 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 \ \ 1 & 1 & 0 & 0 \ край \ вдясно) [/ math]