ИЗСЛЕДВАНЕ НА ПРИЛОЖЕНИЕТО НА РАЗПРЕДЕЛИТЕЛНИТЕ ФУНКЦИИ С ПРИЛОЖЕНИЕТО НА АПАРАТА НА "СВЪРЗАНИ" ФУНКЦИИ -

При изучаване и апроксимиране на функциите на разпределение f (x) чрез сумата на амортизирани експоненциални показатели, основната цел беше да се получи най-доброто приближение. Чрез приближаване на сумата на амортизираните експоненциални показатели се постига най-доброто приближение в така наречената „тежка” опашка на разпределението. Апроксимация на произволна плътност на разпределение, която описва поведението на реален поток от пакети (трафик), ви позволява да анализирате аналитично характеристиките на мрежата. На първо място, има проблемът с анализирането на пакети по време на тяхното предаване по мрежата; често е невъзможно да се определи какво е максималното закъснение при предоставяне на определена услуга. На второ място, няма методи за изследване на мрежови параметри въз основа на статистически данни за предадения трафик. Една от основните задачи на висококачествената работа и управление на мрежата е необходимостта да се контролират и прогнозират предварително основните характеристики на мрежата: забавяне, трептене, процент загубени пакети, честотна лента и други.

Докладът представя изследване на разработения алгоритъм за решаване на интегралното уравнение (IE) на Линдли чрез спектралния метод за система за масово обслужване (QS) от типа G/G/1, базиран на апроксимации, използващи сумата на амортизираните експоненциални показатели. Това сближаване позволява да се получи израз за функцията за разпределение на времето за изчакване и за средното време за изчакване на пакет в опашката.

Въпреки това, когато се анализира апроксимацията чрез сумата на амортизираните експоненциални стойности, възникна проблем при минимизиране и намаляване на грешката на апроксимация до нула. Получените резултати от изследването, използвайки примера на разпределенията на "тежката" опашка (PTX), доказват, че приближаването на произволна функция на плътността на вероятността чрез сумата на амортизираните експоненциални показатели е целесъобразно, тъй като получените теоретични априорни оценки на грешката е минимална. Но, използвайки примера на функцията за разпределение на Weibull, може да се види, че проблемът остава неразрешен в началния раздел на сближаването, тъй като приближението чрез сумата на амортизираните експоненциални показатели описва слабо изследваната функция в раздела близо до нула.

Поради това беше направен опит за изследване на два раздела от функцията за разпределение, така наречените „зашити“ функции за разпределение.

Има функция на Weibull f (x), която приближаваме по участъците от (0, x0) до (x0, ∞), за по-точно решение на Lindley IE, за да се намали грешката на приближение R (x) → 0.

Плътността на функцията за разпределение на Weibull има следната форма (фиг. 1):

(един)

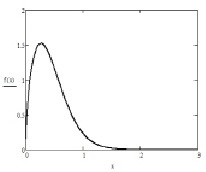
Фигура: 1. Функция на плътността на разпределение на Weibull за α = 1,6 и β = 0,5

Както се вижда от фиг. 2 близо до нулата има проблем с лоша апроксимация от сумата на амортизираните експоненциални стойности, така че ще апроксимираме функциите поотделно и след това ще ги „зашием“ [1].

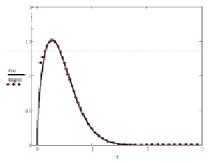
Фигура: 2. Сравнение на две плътности на разпределение по Weibull

Представяме приближението на f (x) на отсечката (0, x0) чрез полиноми:

Разглеждаме апроксимацията на f (x) върху отсечката (x0, ∞) чрез сумата на амортизираните експоненциални показатели [2, 3]:

Наложително е да се вземе предвид условието за нормализиране и за двете части на функцията "зашити".

Помислете за "зашиване" на функции в една [1]:

(2)

Вземаме предвид нормалното условие

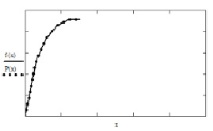
Фигура: 3. Апроксимация на функцията за разпределение на Weibull f (x) върху сегмента (0, x0) с полиноми

Необходимо е да се "съединят" две функции φ1 (x) и φ2 (x) в една φc (x) и след това да се намери преобразуването на Лаплас за решаване на IE Lindley по спектрален метод [2, 3].

(3)

където A (s) и B (s) са трансформацията на Лаплас на плътността на разпределение на интервалите от време между пристигането на пакети и плътността на разпределение на времето за обслужване, съответно.

Аналитичен изглед на функцията "зашита":

В нашия случай получаваме:

тъй като функцията на Weibull f (x) съществува на интервал от (0, x0).

В нашия случай вземаме a = 0, b = ∞ и получаваме интеграл от формата (4)

(4)

За функцията на Weibull f (x), апроксимирана от полиноми на сегмента (0, x0), имаме (5):

, (пет)

Където .

За функцията на Weibull f (x), апроксимирана от сумата на разпадащите се експоненциални показатели в сегмента (x0, ∞), имаме (6):

(6)

Където .

Пример за "зашити" функции

Да разгледаме случая, когато интервалите от време между пристигането на пакети имат разпределение на Weibull с параметрите α = 1.6 и β = 0.5, а интервалите от време за обслужване имат разпределението на Парето с параметрите α = 1.5 и β = 1. Експериментално определете точката x0, при което се достига максималната стойност на функцията за разпределение на Weibull за дадените параметри, в този случай x0 = 0,3.

В съответствие с алгоритъма за апроксимация чрез сумата на амортизирани експоненциални стойности, след получаване на преобразуването на Лаплас I на "зашитата" функция е необходимо да се реши Lindley IE чрез спектралния метод.

A (s) е трансформацията на Лаплас на плътността на разпределение на времевите интервали между пакетите от функцията на Weibull. Трансформацията на Лаплас на зашитата функция е I = A (s), B (s) е трансформацията на Лаплас на плътността на разпределение на времето за обслужване от функцията на Парето:

Решаваме Lindley IU, използвайки спектралния метод [2], получаваме функцията на времето за изчакване на пакетите в опашката W (t):

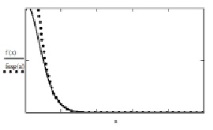
Фигура: 4. Апроксимация на f (x) върху сегмента (x0, ∞) от сумата на амортизираните експоненциални стойности

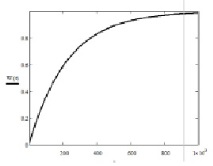
Фигура: 5. Функция на времето за изчакване на пакети в опашката W (t)

констатации

Въз основа на този резултат можем да заключим, че разделяйки на раздели приближението на функцията за разпределение, описващо интервалите от време между пристигането на пакети, дава минимална грешка. Необходимо е обаче да се разгледат няколко вида сближаване на обект близо до нулата и да се сравнят най-добрите решения на Линдли по спектрален начин, за да се определят средните характеристики на мрежата.