Симплекс - алгоритъм (2-ри етап на симплекс - метод)
Основна теорема на симплексния метод.
Симплекс - методът се състои от два етапа:
1) намиране на първоначалното референтно решение на LPP;
Намиране на оптималното решение. Този етап се нарича симплекс - алгоритъм.
Намиране на оригиналното решение за поддръжка (1-ви етап от симплекс метода).
Помислете за LPP в стандартна форма, преместете неизвестните в целевата функция наляво и разгледайте следния проблем.
xj ≥ 0, j = и макс Z., (1.1)
(1.2)
Коментирайте.Свободният член в уравнението на целевата функция е равен на нула, но може да бъде и е различен от нулата.
Ще приемем, че системата (1.1), (1.2) е последователна, системата от уравнения (1.2) е линейно независима и всички .
Нека намерим решението за поддръжка на система (1.2) чрез извършване на последователност от симплексни преобразувания и нека, в този случай, i-f уравнението на системата (1.2) се оказа разрешено по отношение на променливатаxi (i = ):
xi + цел+единxm+един + прицелвам се+2xm+2 + . + aisxs +. + ainxn = bi (i = ), (1.4)
къде са всички bi>0 (i =).
Основните променливи са променливите хедин, х2, ., xm, и безплатно: xm+един, xm+2, ., xs,., xn (основното може да не е непременно първото м променливи). Оригиналното недегенерирано решение за поддръжка на системата (4.4) има формата:
Ще кажем, че системата от уравнения (4.4) се свежда до референтното решение. Изключваме основните променливи от уравнението (4.3). За това всеки i-e, умножаваме уравнението на системата (1.4) по ci и след това добавете всички получени уравнения, получаваме:
(1,5)
Уравнение (4.3) се записва, както следва:
Z– - см+единxm+един - . - csxs -. - cnxn = 0.
Добавяйки това уравнение с (4.5), получаваме:
Ние обозначаваме:
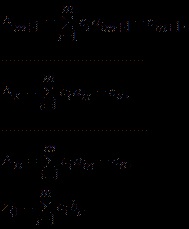
Тогава уравнението на целевата функция ще има формата
Уравнение (4.6) ще се нарича уравнение на целевата функция, редуцирано до свободни променливи, а коефициентите Δj (j = ) - оценки на свободни променливи, където
(1.7)
В резултат на тези трансформации LPP (1.1) - (1.3) се свежда до следния еквивалентен проблем: намерете стойностите
xj ≥ 0, j = и max Z, (1.1)
Задача (1.1), (1.4), (1.6) ще се нарича LPP в канонична форма или в канонична форма.
Системата от ограничения за този проблем се свежда до референтното решение:
Уравнението на целевата функция се свежда до свободни променливи.
Коментирайте.Уравнение (1.6) се добавя към системата от уравнения (1.4) и ние разглеждаме система от (m + 1) уравнения, докато в уравнение (1.6) основното е свободното
Симплекс - алгоритъм (2-ри етап на симплекс - метод).
В задача (1.1), (1.4), (1.6) задаваме свободни променливи, равни на нула, и получаваме оригиналната поддръжка за негенерирано решение (недегенериран дизайн):
Сега от това решение (план) е необходимо да се премине към друго референтно решение (план) X1 с по-голяма стойност на целевата функция от z0, т.е. Z.(хедин) > Z(х0) = Z0.
Да предположим, че за това искаме да въведем безплатна променлива в основата xs = 0, тези. искате да увеличите стойността xs. Освен това в с-m колона трябва да има поне един коефициент ais> 0. Ние избираме с-th колона разрешително.
Преминаваме от едно решение за поддръжка на друго. За да направите това, трябва да изберете разрешаващата линия според правилото
тези. както ще бъде разрешаващата линия r, и като решаващ елемент: ars.
С разрешаващ елемент ars извършваме трансформацията на системата от уравнения (1.4) и (1.6) по формулите за пълно елиминиране на неизвестни (методът на Йордан - Гаус) и намираме ново поддържащо недегенерирано решение X1 със стойността на целевата функция:
Сега ще формулираме правилата за избор на решаващ елемент в симплекс-алгоритъм:
1. В основата въвеждаме безплатна променлива xs с отрицателна оценка Δс 0. Това е правилото за избор на разрешаваща колона с.
2. От основата извличаме променливата xr по правило
Това е правилото за избор на разрешителната линия r.
3. С разрешаващ елемент ars извършваме трансформацията на система (1.4), (1.6).
Неизвестни коефициенти a΄ij, Δ΄j и ценности b΄j, z΄0 в новата система от уравнения се изчисляват по формулите:
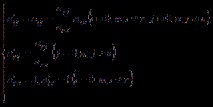
където е въведено обозначението:
Действия, предприети в т. 1-3 съставят една операция на симплекс алгоритъма, след завършване на която преминаваме от референтното решение X0 към X1, докато Z.(хедин)> Z(х0) = Z0.
По този начин коефициентът Δс характеризира промяната в целевата функция Z., на единица промяна в променлива xs, тези. оценява промяната в целевата функция Z.. Следователно коефициентите Δj и се наричат оценки на свободните променливи.
След приключване на една операция можем да преминем към следващата и след поредица от итерации ще получим оптимално решение или ще се уверим, че целевата функция е неограничена. Тези признаци са установени от основната теорема на симплекс метода.
Формулировка: Ако след извършване на следващата итерация:
1) има поне една отрицателна оценка Δs 0, тогава решението може да бъде подобрено чрез извършване на следващата итерация;
2) има поне една отрицателна оценка Δs 0. Следователно новото решение за поддръжка ще бъде по-добро от предишното.
В присъствието на ais>0 стойността на Xs е ограничена от минимума на съотношенията за ais>0. Ако всички ais≤0, след това стойността Xs не можете да ограничавате, защото за произволно голяма стойност Xs, стойностите на всички други основни променливи Xi винаги ще бъде неотрицателно, защото Xi = bi - aisXs и в ais ≤ 0, Xi винаги позитивен.
Така че променливата Xs може да се придава произволно голямо значение и в същото време на целевата функция z също ще достигне произволно голяма стойност, т.е. Zmax → ∞.
3) Ако всички оценки Δj ≥ 0, тогава от. Z.(хедин) = Z0 - Δsxs, от това следва, че увеличавайки всяка свободна променлива, ще намалим стойността на целевата функция Z.. Оттук следва, че за никое друго допустимо решение функцията Z. не може да се увеличи, т.е. намереното решение е оптимално. Теоремата е доказана.
- Радиологични методи за изследване в гинекологията
- Подове от шперплат, размери и дебелина на материала, етап на изравняване, полагане върху замазка и греди
- Фрактура на стъпалото - методи за лечение и рехабилитация след травма
- Отглеждане на пипер в оранжерия, образуване на храст чрез прищипване
- Методи за тайно изследване на простатата и интерпретация на резултатите