Квантовомеханични вектори и оператори в Хилбертово пространство. Аз

Текстът по-долу е част от книгата „Първа стъпка към квантовата реалност“.

Оказа се, че математическият апарат на квантовата механика води началото си от обичайната класическа реалност.

Следователно ще илюстрираме точно сега, без да се позоваваме на квантовата физика, нейните основни характеристики.

1. Независимост на описанието на реалността от избора на координатни системи.

Физическа реалност, а именно движение на тела, действащи сили, сила на електрическо и магнитно поле и др. съществуват обективно, независимо от нас.

Можем произволно да избираме координатни системи и в зависимост от нашия избор получаваме различни формули. Но зад всички разлики във формулите се крие обективно съществуваща физическа реалност. Следователно е възможно да се опише реалността, свободна от произвол, поради избора на координатни системи, накратко, възможно е инвариант описание на реалността.

Именно на това се основава векторната (и тензорна) алгебра и векторите са обекти на триизмерно евклидово или, просто казано, физическо пространство.

Но ние знаем (вж. Описание на посоките и завоите в триизмерното пространство. III), че посоките на физическото пространство могат да бъдат определени чрез математически обекти на двумерното сложно евклидово пространство. - В тази връзка се отваря друга възможност за инвариантно описание на физическата реалност.

2. Кет и сутиени вектори.

И така, нека има единичен вектор, който определя посоката на някаква физическа величина - сила, вектор на силата на полето, ос на въртене и т.н. Този вектор съответства в двумерното евклидово пространство на вектора

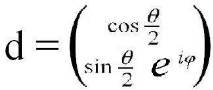
така че d † d = 1.

След умножаването на този вектор по произволно комплексно число с модулен модул, матричните елементи на матрицата d ще се променят, но матрицата d ще продължи да задава същата посока (вж. Описание на посоките и завъртанията в триизмерното пространство. III).

И по-нататък. Нека завъртим координатната система по произволен начин. Известно е, че матриците на въртене са както следва (вж. Описание на посоките и завъртанията в триизмерното пространство. II):

В резултат на това получаваме матрицата d ′ = Ud, тук U е или една от матриците Uх(α/2), UY.(α/2), UZ.(α/2), или всеки продукт от тях.

И отново, въпреки факта, че d и d ′ = Ud са напълно различни матрици, те представляват една и съща посока (пасивна интерпретация).

Следователно има естествено желание да се изобразят всички видове матрици, изобразяващи една и съща посока по еднакъв начин, т.е. е инвариант, например, по следния начин: | d ›.

| d ›се нарича кет вектор.

Тъй като матриците d съответстват на добре дефинирани ермитови конюгирани матрици d †, въвеждаме обозначението | d ›† =‹ d |.

Вектор ‹d | наречен сутиен-вектор.

В резултат на двойно ермитово спрежение всяка матрица се връща в първоначалната си форма. И тъй като обикновените матрици са криптирани с инвариантна нотация, тогава

Сега изразът d † d = 1 може да бъде записан в инвариантна форма:

По-нататък говорим за един вид модификация на векторното смятане, която е разработена от изключителния английски теоретичен физик Пол Дириcom специално за квантова механика.

Изразът "d | d" по същество е скоба. На английски, скоба е скоба. Следователно е ясно защо векторите ‹d | и | d ›се наричат съответно бра-вектори и кет-вектори.

Фактът, че ‹d | d› = 1 означава, че векторът | d ›е нормализиран на един, с други думи, нормата (дължината) на вектора d е равна на единица, r = 1.

Трябва да се подчертае, че само вектори, нормализирани на единство, представляват посоки в триизмерното евклидово (физическо) пространство.

Известно е, че ъгълът между две посоки d1 и d2 се изчислява по формулата (виж Описание на посоките и завоите в триизмерно пространство. VI):

В инвариантна форма формулата приема следната форма:

3. Хилбертово пространство.

Досега ние възприемахме двумерното комплексно евклидово пространство чисто интуитивно - то е подобно на двумерното реално евклидово пространство с единствената разлика: координатите, както и компонентите на векторите, могат да бъдат комплексни числа.

Сега нека дефинираме тази концепция по-ясно.

Матрицата d може да бъде представена по следния начин:

e1 и e2 имат следните свойства: e1 T e1 = e2 T e2 = 1, e1 T e2 = e2 T e1 = 0, или, което е същото,

Тук δ i j е символът на Кронекер. Тя е равна на единица, ако i = j и нула, ако i ≠ j .

Сега, докато разглеждаме най-простите ситуации, въвеждането на общоприети компактни обозначения, като символа Kronecker, сумиращия знак и т.н., изглежда неподходящо. Но сега е време да свикнете с тях, тъй като общоприетата нотация е икономична, те ви позволяват да обобщите много резултати в по-сложни случаи с минимални усилия, може да се каже, автоматично.

Сега нека напишем d в инвариантна форма:

Обърнете внимание, че векторът | d ›е нормализиран на единица,‹ d | d ›= 1. Това условие трябва да бъде изпълнено, за да може векторът | d ›да зададе някаква посока в триизмерното евклидово пространство.

Определение. Наборът от всички вектори от тип

където b 1 и b 2 са произволни комплексни числа, се нарича двумерно комплексно евклидово пространство. Нарича се още хилбертово пространство, защото ако размерът на пространството е краен, тогава двумерното комплексно евклидово пространство и (сложното) хилбертово пространство съвпадат.

По-нататък ще използваме термина „Хилбертово пространство“, защото е толкова по-кратък.

Векторите | e1 ›и | e2› съставляват ортонормалната основа на Хилбертовото пространство. „Орто-“ означава ортогонален, т.е. ‹e1 | e2› = ‹e2 | e1› = 0, „нормализиран“ означава нормализиран до единство ‹e1 | e1› = ‹e2 | e2› = 1.

И така, коефициентите на разширяване на всеки вектор в базисните вектори на Хилбертовото пространство са равни:

Както вече знаем, за да може векторът на Хилбертовото пространство да представлява някаква посока на триизмерното евклидово пространство, е необходимо той да бъде нормализиран до единство. И така, ние изискваме ‹b | b› = 1:

тези. условието за нормализиране за всеки вектор на двумерно хилбертово пространство има вида:

Ако имате съмнения дали инвариантните изчисления се извършват правилно, не забравяйте, че инвариантните нотации са възникнали от матричното смятане, следователно всички правила за операции с матрици са валидни за тях.