SavePearlHarbor

Още едно копие на хабора

Главно меню

След навигация

Теорема за факторизиране за естествени числа

Произволно съставно естествено число N чрез последователно извършване на някои елементарни преобразувания върху него може да бъде представено чрез произведение на формата
N = 2 t2 ∙ 3 t3 ∙ 5 t5 ∙ (pk + 30 ∙ t), където 0 ≤ ti, i = 2,3,5, t - естествено, рk> 5 - просто.
Теорема
1. Ако N е съставно четно естествено число, то то може да бъде представено като N = 2 t2 ∙ n2,
където n2 ≡ 1 (mod 2) е съставно нечетно число, t2 = 1 (1)… и 2 ∤ n2;
2. Ако N = n2 е съставно нечетно число, завършващо на цифра 5, тогава то може да бъде представено като N = 5 t5 ∙ n5, където n5 е съставно нечетно число, t5 = 1 (1)…; и 5 ∤ n5;
3. Ако N = n5 е съставно нечетно число, което не завършва с цифрата 5, а неговото конволюция s (N) (сумата от цифри) е кратно на 3, тогава може да бъде представено като N = 3 t3 ∙ n3, където n3 е съставно нечетно число, t3 = 1 (1)…; и 3 ∤ n3;
4. Ако N = n3 е съставно нечетно число, с последната цифра (флексия) ф ϵ, тогава той има формата N = (pk + 30 ∙ t), където t = 1 (1) ... е естествено число, и pk ϵ, и факторизацията може да се извърши, например, като се използва концепцията на граничен контур и φ-инвариант нечетно число или един от съществуващите известни методи.

Вместо доказателство. Освен това текстът на работата, включително Таблица 3, по същество е доказателство за първата част на теоремата (относно представянето на число под формата на модел N = 30 ∙ t + pk). В хода на презентацията има пълни и пресечени модели на LSP, плоски и обемни. Наборът от всички естествени числа е разделен на две подмножества. Първата - интуитивно възприемана като по-голяма, съдържа естествени числа, които се факторизират с елементарни средства (използват се най-простите критерии за делимост от прости числа 2, 3, 5). Второто подмножество е по-малкото, което също съдържа всички нечетни прости числа (с изключение на 3 и 5), и факторизирането на които представлява непреодолим проблем на съвременността, особено за големи числа. Последният факторизиран номер, известен от публикациите, е описан с 232 десетични цифри.
Известният аналитичен модел на LSP под формата на списък от 30k, 30k ± 1, 30k ± 3, ..., 30k ± 15,
k = 1 (1) ∞, релациите ни позволяват да разберем как можем да опишем тези от числата, които трябва да се съдържат във всеки от посочените подмножества, т.е. по същество изпълняват такъв дял на LSP.
Мултипликативното представяне на числото 30 е 30 = 2 ∙ 3 ∙ 5. Естествени числа N, сравними с нула по модул делителите на 30, N N 0 (mod2), N ≡ 0 (mod3), N ≡ 0 (mod5) са четни числа, числа, делими на три без остатък, и нечетни числа, завършващи на 5.
Оказва се, че множеството естествени числа с нарушение на подобни свойства се разделя на класове на еквивалентност с други прости, добре различими характеристики. По този начин задачата в работата е да раздели LSP на две подгрупи и да получи описание на по-малкия в проста и удобна форма за по-нататъшна обработка на числата.
Класове на естествени числа. Нека вземем за основа на разглежданата класификация два много просто дефинирани показателя за свойства (s, φ) на числата. Първият индикатор се обозначава със s,
1 ≤ s ≤ 9, име конволюция (това е сумата от цифрите на числото, доведени до една цифра) на числото, то характеризира свойството на делимост на числото на три, а вторият индикатор се обозначава със символа f,
0 ≤ ф ≤ 9, - име флексия (крайни, последна цифра) числа, характеризира свойството на крайно число да има последната цифра.

Пример 1. N = 4757, s (N) = ((4 + 7 + 5 + 7 = 23) → (2 + 3)) = 5; φ (N) ≡ N (mod10) = 7.
Двойка свойства на числата, характеризиращи се с индикатори (s, ф), разбиват LSP на несъединени класове (еквиваленти), които имат същите стойности на двойка индикатори. Характеристика на класа числа, към който принадлежи числото N = 4757, е двойка със стойността (s, φ) = (5, 7).
Броят на T (s, f) брой класове, различимо от такава характеристика, се определя от произведението на диапазоните на промяна в стойностите на всеки индикатор на двете свойства на числото
T (S, F) = S × F = 9 × 10 = 90.
Обхватът на всеки клас включва безкраен брой естествени числа, сред които има най-малкото число в класа. Поставяме най-малките представители от всички класове в лявата част на Таблица 1, а отдясно я продължаваме, като попълваме (според модела вляво) клетките на таблиците в ред със следните естествени числа.

Таблица 1 - Класове T (s, f) на числа с период от 90. Самолетен модел на LSP

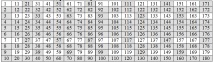
Анализът на съдържанието на таблицата (набор от числа Т-90) показва, че в лявата част на таблицата 10 × 9 всички числа са най-малките в своя клас и имат различни стойности на характеристиката (s, f ). Дясната страна на таблицата 10 × 9, подобно на лявата страна, е изпълнена с представители на различни класове със същите характеристики (s, f), но със следващата стойност (период) на елемента, увеличена с 90 единици. Такива таблици могат да бъдат продължени за неопределено време и преместени вляво, припокриващи 1-ва (лява) таблица. В резултат на това получаваме триизмерен паралелепипед, в който всички числа са написани над всяка клетка от долната таблица, които образуват класа на естествените числа с фиксирана стойност на двойката (s, φ).

Обемен LRF модел

По същество получихме още един обемен модел на LSP. Неговите предимства се проявяват в способността да се намали значително LRF, без да се губят важни позиции, например позиции, съдържащи прости числа. Нека да покажем как това може да се направи.
Първо, изтриваме редовете от таблица 1, съдържащи четни числа и нечетни числа, завършващи на пет, и второ, премахваме класовете числа, кратни на три. Клетките на таблицата от такива класове принадлежат към диагоналите, успоредни на страничния диагонал на таблицата. В таблица 1 изтритите клетки (класове) са маркирани със запълване.
Незасенчените клетки-класове T (s, f), броят на които са 24 (останалите след изтриване на числата, ще наречем множеството T-24), са запазени, те съответстват на клетките на таблицата без попълване. Възможните инфлексии в останалите класове ще бъдат само φ = 1,3,7,9 и при всяка инфлексия 6 стойности на конволюцията, т.е. 24 класа. Съвсем очевидно е, че прости числа могат да се появят само в тези класове. Всъщност в лявата таблица от 24-те най-малки представители от всички класове 22 са прости числа. Само две клетки (от 24) са запълнени със съставни числа 7 × 7 = 49 и 7 × 11 = 77, получени чрез умножаване на най-малкото оставащо просто число 7 по себе си и по следващото просто число 11.

Алгебрична група от остатъци на генератори на класове

Ще продължим да реформираме NRM, връщайки се към числото 30 = 2 ∙ 3 ∙ 5. Спомнете си, че осемте прости числа p (i) = образуват мултипликативна група E (група на Ойлер) от остатъци от осми ред по модул на това. Елементът за идентичност се идентифицира с прости 31, p (i) ≡ 31 (mod30) = 1. Съгласно теоремата на Лагранж (за групови поръчки), групата може да има правилни подгрупи от 2-ри и 4-ти ред. Елементите от група 8-ми ред (11,19 и 29) са от 2-ри ред; (7,13, 17, 23) 4-ти ред и един. Има три подгрупи от 4-тия ред: една (1,11,19,29) - включва само инволюции и две подгрупи са циклични:
7 × 7 ≡ 49 (mod30) = 19; 19 × 7 ≡ 133 (mod30) = 13; 13 × 7 ≡ 91 (mod30) = 1;
11 × 19 ≡ 209 (mod30) = 29; 11 × 29 319 (mod30) = 19; 19 × 29 ≡ 551 (mod30) = 1;
17 × 17 ≡ 289 (mod30) = 19; 19 × 17 ≡ 323 (mod30) = 23; 23 × 17≡ 391 (mod30) = 1;

Изненадващо, но всички числа от 24 класа | Т (S, Ф) | = 3 × 8 се трансформират в семейство от класове, състоящи се от общо 8 класа, генерирани от всеки представител на множеството p (i). В новите класове числата - елементи следват с период не 90, а три пъти по-малко, само 30.

Таблица 2 - Мултипликативни подгрупи на групата на остатъците (pk) mod30

Класовете се формират, като се вземат предвид извиването и свиването на числата в три двойки (2,1), (5,1), (8,1); (4.1), (7.1), (1.1); (2.3), (5.3), (8.3); (4.3), (7.3), (1.3); (7.7), (1.7), (4.7); (8,7), (2,7), (5,7); (7,9), (1,9), (4,9); (8,9), (2,9), (5,9);
По-долу в таблица 3 даваме първоначалните фрагменти от тези 8 класа. Всяко нечетно число N> 31, което не е кратно на 3 или 5, има формата N = p (i) + 30t и попада в един от 8-те класа, представени в Таблица 3. Нека наречем множеството от числа от такава таблица комплект Т - 8.

Таблица 3 - Класове числа с период от 30. Простите числа k> се подчертават чрез попълване

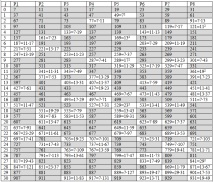
Дори бегъл анализ на таблицата ни позволява да направим някои изводи по отношение на простотата-сложност и възможността за разлагане на числа на фактори:
- всички степени на генераторите на всички класове, т.е. прости числа - съставни;
- редове с число, кратно на генератора в клетката на колоната на този генератор, съдържат съставни числа, чийто делител е генераторът;
- числа, принадлежащи към зоната на забрана на прости числа в спиралата на Улам - съставни, примери за такива числа през първата хиляда: 143,161,203,217,323,451, 517,539,473, 611,637 и др.
- числа, които могат да бъдат разложени на сума-разлика и скоби на общ фактор, например 217 = 210 + 7 = 7 (30 +1) = 7 × 31; 1397 = 1270 +127 = 127 (10 +1) = 127 × 11.
По този начин чрез елементарни средства и операции е възможно да се избере набор от нечетен брой Т-8 на Т-8, който трябва и може да служи като обект на последващо изследване в интерес на решаването както на теоретични, така и на приложни практически проблеми. Такива проблеми в областта на криптологията и информационната сигурност включват следното: ZFBCH, проблемът за установяване на простото число, проблемът с дискретния логаритъм в крайни полета и групи точки от елиптични криви.
Наборът от числа T-8 е организиран по специален начин (състои се от 8 класа), като най-малките представители на класовете образуват група остатъци по модул 30 (φ (30) = 8). Това свойство определя номера на колоната на резултата от произведението на двойка числа, чиито номера на колони са известни. Таблицата за групи Keli предоставя решение на този проблем.
Целта на примерите е да покаже каква информация за връзките на стойностите на числата, номерата на редовете и номерата на колоните се съдържа в набора T-8.
Един от възможните методи за разлагане на числа на множеството Т-8 с помощта на таблица 3.
Пример 2. Нека съставено нечетно естествено число (cnch)
N = 1727. Искате да го разделим на фактори. Нека намерим позицията на това число в множеството T-8: номер на ред N/30 = 57 (взема се цялата част от фракцията), номер на колона (име) N - 30 ∙ 57 = 17. В същата колона ние задайте произведението 7 ∙ 11 = 77, число, чийто ред е 2.
Опитва се да задържи всеки от делителите. Запазваме d1 = 7, другият делител N приема формата
d2 = 11 + 30 ∙ t, където t се определя чрез разликата в номерата на редовете и съхранения делител
t = (57 - 2)/7 = 7,85. Получихме дробна стойност, от която следва, че 7 не е делител на дадено число 1727. Всъщност можете веднага да разберете чрез пробно деление дали di е делител на дадено число.
Запазваме d2 = 11, друг делител приема формата d1 = 7 + 30 ∙ t, където t се определя чрез разликата между номерата на редовете и запазения делител t = (57 - 2)/11 = 5. Тогава d1 = 7 + 30 ∙ t = 157.
Всъщност 1727/157 = 11.
Пример 3.Нека съставено нечетно естествено число (cnch)
N = 4294967297, извън таблицата. Искаш да го разделиш на фактори. Намерете, както преди, позицията на това число в комплекта T-8:
номер на реда N/30 = 143165576,
номер на колона N - 30 ∙ 143165576 = 17.
В същата колона задаваме продукта 7 ∙ 641 = 4487, чийто номер на ред е 149.
Опитва се да задържи всеки от делителите. Запазваме d1 = 641, другият делител приема формата
7 + 30 ∙ t, където t се определя чрез разликата в линиите и съхранения делител
t = (143165576 - 149)/641 = 143165427/641 = 223347.
Стойността t = 223347 е цяло число, следователно 641 е делителят на първоначалното число N.
Всъщност, N/d1 = 4294967297: 641 = 6700417 - просто число (различен делител).