Елементи на проективната геометрия Перспективна и проективна геометрия

Конични сечения

Това означава, че всички разсъждения и доказателства, при които се срещат бисектриси, перпендикуляри, кръгове, не могат да се използват в проективна геометрия. Всичко, което можем да си позволим, е сложна връзка между точки и прави линии, по-специално хармонични четворки. И на първо място е необходимо да се намери проективен аналог на кръга.

Помислете за централната проекция на окръжността върху равнината. Сноп от проекционни линии образува конична повърхност.

Следата, която тази конична повърхност образува, когато се пресича с равнина, е централната проекция на кръга. От геометрията на Евклид е известно, че коничните сечения са от три различни типа: елипса, парабола, хипербола.

От проективна гледна точка няма разлика между тях. Единствената разлика е в относителното положение на коничния участък (или, както често казват "коничните") и безкрайно отдалечената права линия. Елипсата е конично сечение, пресичащо безкрайно далечна права линия, парабола е конично сечение, докосващо безкрайно далечна права линия, и хипербола, ако пресича безкрайно далечна права линия. Асимптотите на хипербола са допирателни в безкрайните точки.

Тъй като линията в безкрайността не се различава от която и да е друга права линия в проективната равнина, няма разлика между елипса, парабола и хипербола на проективната равнина.

Сега нека дефинираме полюса на точка по отношение на произволно конично сечение. Тъй като за всяка проекция хармоничната четворка остава хармоничната четворка, дефиницията няма да претърпи значителни промени.

Взимаме произволна точка А на проективната равнина и чертаем през нея всички линии, пресичащи коничния разрез. За всеки хорд МР ще конструираме точка B, така че точки AB, МР да образуват хармонична четворка. Всички такива точки лежат на една права линия, която се нарича полюс на точка А спрямо коничния разрез. Всъщност с централната проекция кръгът преминава в коничен разрез, хармонична четворка - в хармонична четворка, права линия - в права линия.

За да се конструира полярна, би могло да се използва допирателна към коничен участък, поне в случая, когато полюсът лежи извън коничната, но ние ще направим обратното. Използваме независима конструкция на полюса, за да изтеглим допирателни към коничния участък.

Изграждане на полярна с една владетел

Всъщност от всяка страна на четворката се формира хармонична четворка. Например диагоналът AB пресича страните на четирите върха в точките, които заедно с точката C хармонично разделят краищата на двете хорди на коничния разрез. Следователно, линията AB е полярната точка на точка C. По същия начин линиите AC и CB са полярите на точките C и A.

Три връх ABC се нарича автополярен три връх на коничен разрез, тъй като всяка страна от него служи като поляр на противоположния връх.

Полученият чертеж може да бъде възпроизведен, като се започне от една от точките A, B или C. Достатъчно е да се начертаят две прави линии през него, които пресичат кониката в четири точки, и след това да се допълнят останалите страни и диагонали на четири- връх. Сега можем да изградим поляр на която и да е точка спрямо всеки коничен участък. По този начин, ако е дадена точка извън коничния разрез, можете да конструирате две допирателни с помощта на една линийка.

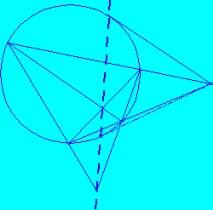
Тази конструкция може да се приложи с еднакъв успех на парабола, хипербола или елипса и по-специално на кръг. Фактът, че допирателните към окръжност наистина могат да бъдат конструирани по този начин, отново е много труден проблем от "класическата" геометрия. Във всеки случай тази конструкция не е била известна на древните геометри.

Често поради технически причини се използва малко по-различна конструкция, която не излиза далеч отвъд обиколката (коничен разрез).

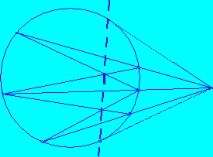
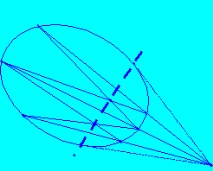
Забележете също така, че сега всички проективни свойства на полярното и полярното преобразуване могат да се считат за доказани за произволно конично сечение на проективната равнина. Ако например е известно, че на евклидовата равнина полярната трансформация по отношение на окръжност запазва сложна връзка, тогава след изграждането на централна проекция върху която и да е друга равнина, ще видим, че окръжността ще стане конична, полюсите и полярите ще останат полюси и поляри и ще останат всички сложни отношения. Това означава, че твърдението на теоремата ще остане вярно.

Повече за вписания четири връх

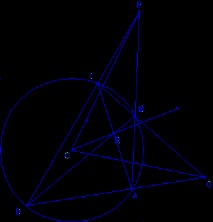
Изчертавайки три диагонала на вписания четиривершен ABCD, получаваме автополярен тривръшен PQR. Всеки от върховете му е полюс на противоположната страна. Това означава, че полярният PQ е перпендикулярен на линията ОR, свързваща полюса R и центъра на окръжността O. По същия начин линиите PR и OQ, както и QR и OP, са перпендикулярни. Елиминирайки полюсите и полярите от формулировката, получаваме теоремата на Брокар.

Нека точки A, B, C, D лежат на окръжност, а двойки прави линии AB и CD, BC и AD, AC и BD, съответно, се пресичат в точки P, Q, R. Тогава височините на триъгълника PQR се пресичат в центъра на кръга.

ДА СЕ

Разбира се, възможно е (по принцип) да се докаже тази теорема, без да се извиква проективна геометрия, като се използват „училищни“ методи. Опитвам!

Ето още една теорема, която може лесно да бъде получена с помощта на полюси и поляри. Вземете четири точки A, B, C, D върху окръжност (коничен разрез). Нека линии AB и CD се пресичат в точка S, а линии AC и BD - в точка M. Както знаете, полярната точка на точка S преминава през точка М.

В същото време от принципа на двойствеността следва, че полюсът на точката S може да бъде конструиран чрез свързване на полюсите P и Q на линии AB и CD. Тези полюси са лесни за намиране, тъй като пресечните точки на допирателните в върховете A, B и C, D. Следователно точките P, Q, M лежат на една права линия.

Прилагайки същата конструкция към линии AD и BC, получаваме следната теорема:

Ако четири кръг е описан около кръг (коничен разрез), тогава правите линии, свързващи точките на допир на противоположните страни и диагоналите на квадрата, се пресичат в една точка.
Тази теорема, разбира се, може да бъде доказана по обичайния начин, като се използва сходството на триъгълниците. В допълнение, в следващото ще бъде доказана теоремата на Брайъншон, за която теоремата за описания четириверх е естествен специален случай.
Нека сега се опитаме да приложим теоремите, доказани за изследване на свойствата на хиперболата. Спомнете си, че хипербола е коничен участък, пресичащ линията в безкрайност. Допирателните в две точки в безкрайността се наричат асимптоти на хиперболата.

З.

а евклидовата равнина, хиперболата и окръжността са две различни криви от втори ред. От проективна гледна точка няма разлика между тях. Те просто са позиционирани по различен начин спрямо наблюдателя. Всички проективни свойства на окръжността също ще бъдат проективни свойства на хиперболата, параболата и елипсата.

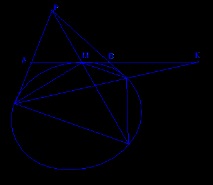
Нека асимптотите на хиперболата се пресичат в точката P, полюса на линията в безкрайност. Изчертаваме допирателна в произволна точка М. Тази допирателна пресича полюса на точката P и две допирателни, изтеглени от точката P, в точките A, B, K, така че AB, MK е хармонична четворка (защо?). Това важи за всяка точка P, разположена извън коничния разрез.

Но ако точка K е безкрайно отдалечена, тогава точка M, както знаете, ще бъде средата на отсечката AB. Получаваме теоремата:

Сегментът на допирателната към хиперболата, отрязан от асимптотите, се разделя на допирателната точка наполовина.

Друго важно свойство на хиперболата може да бъде получено с помощта на теоремата за описания четиривърх.

Да разгледаме ABCD с четири върха, чиито страни са две допирателни и две асимптоти (също допирателни). По силата на доказаната теорема линии AC и BD се пресичат в точка, разположена на права линия, свързваща точките на допир на хиперболата с линии AD и BC, тоест в точката в безкрайност.

Това означава, че прави линии AC и BD са успоредни. Следователно площите на триъгълниците ABC и ADC са равни, което предполага равенството на областите на триъгълниците ABC и CDP. Така че теоремата е вярна:

Триъгълникът, образуван от асимптотите на хиперболата и произволна тангента, има постоянна площ.