28 март 2017 г. - - Бележки по - теоретична физика

Нека продължим да решаваме „проблема с хокея“. В последния пост разгледахме вариант на проблема с изкуствена поддръжка на постоянна скорост на въртене на пръстена. Нека сега се обърнем към варианта, когато поради триенето се забавя не само транслационното движение, но и въртенето.

Припомняме, че динамиката на пръстена се описва от уравненията

където $$ v $$ е скоростта на транслационното движение, $$ u = \ omega R $$ е скоростта на въртеливото движение на пръстена.

Системата от уравнения (1) е симетрична по отношение на заместването на $$ u $$ с $$ v $$. Ако в началния момент $$ u = v $$, то от съображения за симетрия това съотношение ще остане между скоростите до един стоп. Друг случай, който ще разгледаме, е $$ u> v $$. Обратен случай $$ u v

За съжаление интегралите в системата (1) се свеждат до елиптични, което не оставя надежда за аналитично решаване на системата. Цифровото решение остава.

Директният опит за решаване на уравнението в Maple се проваля. Определените интеграли са заменени от куп елиптични интеграли, което няма смисъл да се представя тук. Когато изчертаваме диаграмата, виждаме съобщение за грешка

За да опростим изразите, налагаме ограничението $$ u (t) \ ge v (t) \ ge 0 $$ на всеки от интегралите.

Ограниченията премахват съобщението за грешка. Maple отнема много време да мисли, но показва празна графика. За да разберем причината, извеждаме решението на уравнението в даден момент.

$$ [t = 1., \\ u (t) = 10.9976102709142-2.84005015829721 10 ^, \\ v (t) = 1.04887416587408 + 2.92542849266058 10 ^] $$

Натрупването на грешка при закръгляването води до появата на ненулева въображаема част в търсените функции, поради което графиката е празна. За да избегнем появата на въображаемата част, вземаме изрично реалната част от дясната страна на уравненията:

И накрая, Maple, след дълъг размисъл, все още рисува графика.

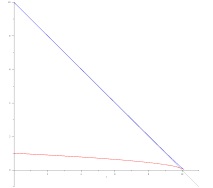
В същото време виждаме предупреждение за точката на спиране на изчисленията, което очевидно съвпада с момента, в който движението завършва:

Предупреждение, не може да се оцени решението по-нататък вдясно от 10.155665, вероятно сингулярност

За числовото решение избрахме начална скорост на транслация 1 и скорост на въртене 10. Без въртене, пръстенът се движи в рамките на 1 единица време с разстояние 0,5. Наличието на въртене доведе до факта, че транслационното движение се поддържаше повече от 10 единици време.

Линеаризирано решение за u >> v

Графиката $$ u (t) $$ - синята линия - практически съвпада с правата линия. Графиката $$ v (t) $$ - червената линия - прилича на парабола. Това поведение се предвижда от линеаризираното решение в границата $$ u \ gg v $$. Пренебрегвайки $$ v $$ в първото уравнение на системата (1) и разширявайки второто по степен на $$ p = v/u $$, получаваме

Решението на тази система е функциите $$ u (t) = u_0-t $$, $$ v (t) = v_0 \ sqrt $$. Графиките им са показани в сиви линии.

Както можем да видим от числовото решение и графиката, приближението правилно описва естеството на движението, докато $$ u $$ и $$ v $$ станат сравними. Ето графика за случая, когато едната скорост е два пъти друга:

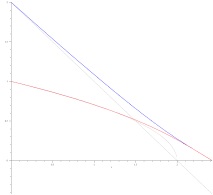
Тук разликата от линеаризираното решение се забелязва почти веднага.

Път към спиране: Линеаризирана апроксимация

Пътят, изминат от пръстена, се дава от площта на извития трапец под червената линия. В линеаризираното приближение криволинейният трапец е ограничен от парабола и, както е лесно да се види, има площ $$ l = 2u_0v_0/3 $$. Ако пръстенът не се върти, той ще измине разстоянието $$ l_0 = v_0 ^ 2/2 $$. По този начин, за да увеличите проходимата пътека с 5 пъти, трябва да завъртите пръстена с ъглова скорост

Спомнете си, че за да може пръстенът да премине една и съща пътека, като същевременно запази въртенето, скоростта му трябва да бъде три пъти по-малка: $$ \ omega_0 = (5/4) \, $$.

Път към спиране: Числово решение

Сега изчисляваме преминаващия път от първоначалните уравнения, без линеаризация.

По някаква причина Maple не намери точка на прекъсване ("сингулярност") за първоначалната стойност 15/4 и неправилно продължи решението. Ние намираме приблизителното положение на тази точка, като избираме.

Maple изчислява последния резултат за 10 минути. Както можете да видите, за началната стойност 15/4 грешката на линеаризираното приближение е 2%.

Решихме "проблема с хокея" в оригиналната опростена формулировка и без опростявания в линеаризираното приближение. С помощта на компютърната алгебрана система Maple се уверихме, че за състоянието на този проблем линеаризираното приближение дава грешка от няколко процента.