1 семестър)

ПРОБЛЕМ 1. Графични примери за функции с определени елементарни свойства. Използвайте "дефиниции".

и характеризират монотонността на функцията.

ПРОБЛЕМ 3. Изследвайте последователност за монотонност.

Ако иn + 1> ан за произволен номер P , тогава последователността е възходяща;

ако иn + 1 0, тогава последователността се увеличава. Примери за

б) За положителен последователности, можем да разгледаме стойността

. Ако тя е по-голяма от единица, тогава последователността е възходяща; ако е по-малка от единица, тя намалява. Примери за.

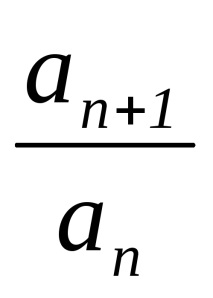
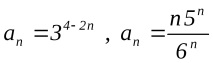
в) Редуващата се последователност не е монотонна. Примери за.

И още два много "дъбови" метода, за особено "надарени". Но можете да се „придържате“ към тях.

г) Изградете "графика" на последователността (това е прекъсната линия) и по естеството на графиката ("нагоре", "надолу") определете естеството на монотонността.

д) Създайте таблица със стойности на последователността и определете естеството на монотонността, като използвате тази таблица.

Изследване за ограничение.

Определение за ограниченост: Ако има такива P

ан  A , тогава последователността е ограничена до ДОЛОТО от числото А;

ан  Б. , тогава последователността е ограничена до ТОП от числото B;

A  ан  Б. , тогава последователността е просто ОГРАНИЧЕНА от числата A и B.

а) Възходящата последователност винаги е ограничена до ДОЛОТО от първия член.

б) Низходяща последователност винаги е ТОП-ограничена от първия член.

в) Последователност, която има граница, винаги е просто Ограничена от теоремата.

В други случаи е полезно да разгледате графиката на последователността и да се уверите, че има (или не) „таван“ или „етаж“.

Когато работите по грешки за задача № 3, трябва да използвате КЛОН:

Изчисляване на множество членове на последователност с командата

Последователност на графика (прекъсната линия)

ПРОБЛЕМ 4. Докажете тази граница по дефиниция.

Пример. Докажете по дефиниция, че .

Първо напишете дефиницията (не използвайте иконите  и ).

Всеки    има номер N ( ), като се започне от кой (т.е. за всички nN ( ) ) неравенството .

Решението на проблема Нека бъде дадено произволно   . Намерете номера N ( ) . За да направим това, нека решим неравенството. По този начин за всеки    намерихме число

, изхождайки от неравенството, както се изисква за доказване.

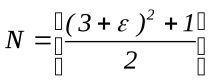
Забележка. Квадратни скоби [A] представляват целочислената част на A.

ПРОБЛЕМ 5. Използване на символи относно(…) и , сравнете последователностите.

За сравнение на две последователности ан и бн границата трябва да бъде намерена

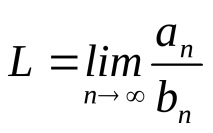
Когато работите по грешки за проблем № 5, трябва да използвате програмата за сравнение на последователности, написана на езика КЛОН: