„Учебник по дискретна математика. Графики на Ойлер и полу-Ойлер "

Именно с проблемите, поставени и решени в този раздел, започна теорията на графовете. Философът Имануел Кант, разхождайки се из град Кьонигсберг (сега този град се нарича Калининград), поставя проблем (1736), известен в математиката като проблем на седем моста на Кьонигсберг: възможно ли е да се преминат през всички тези мостове и едновременно връщане на времето към началната точка, така че всеки мост трябва да бъде преминат само веднъж. Нашият известен петербургски математик от швейцарски произход Леонард Ойлер реши блестящо този проблем. На фиг. 2 показва диаграма на седем моста на Кьонигсберг (имайте предвид, че сега са останали само два от тях), както и мултиграф, съответстващ на тази диаграма (при изграждането на графиката се приема, че всеки речен бряг и остров са върховете на графика, а мостовете са нейните ръбове; можете да видите, че в този случай имаме мултиграф без цикли).

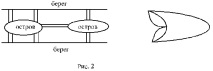
В съответствие с проблема, поставен от Кант (и решен от Ойлер), могат да се дадат следните определения:

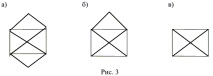
Графика (или мултиграф без контури) се нарича Ойлер, ако има цикъл без повтарящи се ръбове (такъв цикъл се нарича Ойлер), който пресича всички върхове на графиката. Графика се нарича полу-Ойлер, ако има маршрут без повтарящи се ръбове (път на Ойлер), който пресича всички ръбове на графиката точно веднъж. На фиг. 3 показва: a - графика на Ойлер, b - полу-ейлерова графика и c - графика, която не е нито eulerian, нито полу-eulerian (хората от по-старото поколение знаят, че в училищата е имало много загадки като "възможно ли е да нарисувате тази фигура, без да вдигате писалката от хартията ", което съответства на графика на Ойлер или полу-Ойлер).

Теорема (Ойлер). За даден свързан граф (не диграф, но евентуално мултиграф без контури) да бъде Ойлер, е необходимо и достатъчно градусите на всички върхове да са четни. Даден свързан граф ще бъде полу-Ойлер, ако и само ако градусите от два върха са нечетни, а градусите на останалите върхове са четни.

Започваме доказателството на тази теорема с така наречената лема за ръкостискане. Името на тази лема се дължи на факта, че тази лема отговаря на следния въпрос: Имате няколко гости. Някои от тях се поздравяват, като се ръкуват. Какви свойства има броят на такива хора? Отговорът се дава от следната доста проста лема.

Лема за ръкостискане. Броят на върховете в графика (или мултиграф без цикли) с нечетна степен е четен.

Доказателство за лемата. Имайте предвид, че сумата от градусите на всички върхове в графика (или мултиграф без контури) трябва да бъде четна. Това следва от факта, че ако вземем върхове, които изобщо не са свързани помежду си, тогава сумата от градусите на тези върхове е равна на нула. Чрез добавяне на всеки ръб, който свързва два върха, увеличаваме сумата на всички градуси с 2 единици. По този начин сумата от всички степени на върховете е четна. Премахвайки градусите на четните върхове от тази сума, получаваме, че сумата от градусите на нечетните върхове трябва да е четна. Това означава, че самият брой на тези върхове трябва да е четен. Лемата е доказана.

От гледна точка на проблема с ръкостискането, това означава, че броят на гостите, които са се ръкували нечетен брой пъти, трябва да е четен. Нека да преминем към доказателството на теоремата на Ойлер.

А) Нека графиката да е Ойлер. Тогава в него има цикъл на Ойлер, който трябва да стигне до върха по единия ръб и да го напусне по другия, тъй като всеки ръб трябва да се използва само веднъж (т.е. всеки „влизащ“ и „напускащ“ върха дава 2 градуса върхове). По този начин сумата от градусите на всички върхове трябва да бъде четна (и е равна на удвоения брой „вписвания“ в този връх при преминаване на цикъла на Ойлер).

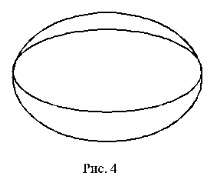
Б) Нека в дадена свързана графика (или мултиграф без цикли) степента на всеки връх е четна (т.е. степента е по-голяма или равна на 2, тъй като нулевата степен води до несвързана графика). Нека докажем, че съдържа цикъл на Ойлер. Доказателството е чрез индукция на броя на върховете. В случая, когато в свързана графика има само 2 върха и двата имат четна степен (в случая имаме мултиграф, единият от които е показан на фиг. 4), е ясно, че в този случай има цикъл на Ойлер (за всяка четна степен на тези два върха).

Да предположим, че нашето твърдение е вярно за всички свързани графи, броят на върховете в които е строго по-малък от n, и ние го доказваме за граф с n върха.

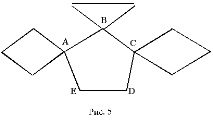
Имайте предвид, че по лема 1 тази графика съдържа контур (степента на всички върхове е по-голяма или равна на 2). Ако този контур съдържа всички ръбове, то самият този контур е цикъл на Ойлер (а графиката е Ойлер). Нека премахнем всички тези ръбове от графиката и онези върхове, които след премахване на ръбовете стават на нулева степен. След това получаваме нова графика (която може да бъде прекъсната), но в тази нова графика всички върхове задължително трябва да имат четна степен (тъй като когато премахнете ръбовете на контура, степента на всеки връх, включен в този контур, намалява с 2 ). Новата графика се разделя на „свързани компоненти“, всеки от които трябва да има общ връх с премахнатия контур (в противен случай оригиналната графика не би била свързана), градусите на всички върхове на всеки свързан компонент са четни и броят на върховете в тя е строго по-малка от n, т.е. индуктивно този компонент има цикъл на Ойлер. Сега можем да изградим цикъл на Ойлер в тази графика, както следва. Последователно обикаляме краищата на изтрития контур. Ако стигнем до връх, общ за контура и някакъв свързан компонент, тогава заобикаляме този компонент по цикъла на Ойлер, връщаме се към върха на контура и вървим по-нататък по този контур. По този начин всички ръбове ще бъдат пресечени и всеки само веднъж (всичко това е показано схематично на Фиг. 5: първо започваме да пресичаме контура ABCDEA. След като преминем AB ръба, предаваме „горната“ графика, след което се връщаме към точка B и след това вървим по AC ръба, заобикаляме „дясната“ графика и т.н.). Изявление Б е доказано.

В) Нека сега графиката да е полу-Ойлер. Това означава, че има пътека на Ойлер, която започва от един връх и завършва от друг. Вижда се, че и двата върха трябва да имат нечетна степен, а степента на останалите е четна.

Г) Назад. Да предположим, че в свързана графика върховете k и p имат нечетни степени, а останалите върхове са четни. Тогава са възможни 2 случая: тези върхове са свързани с ръб или не. В първия случай ще премахнем този ръб, а във втория ще го добавим. И в двата случая степента на всички върхове ще стане четна. Имайте предвид, че ако ръбът бъде премахнат, новата графика може да се разкачи и да има 2 свързани компонента (в този случай премахнатият ръб е мост), всеки от които или цялата нова графика има цикъл на Ойлер. Сега, ако новата графика има цикъл на Ойлер, тогава започваме (и го завършваме) във връх с нечетна степен и след това добавяме ръб или го премахваме. И в двата случая получаваме пътя на Ойлер. Ако новата графика има 2 свързани компонента, след като преминете през един от тях по цикъла на Ойлер, започвайки и завършвайки в върха (който в оригиналната графика е имал нечетна степен), тогава добавяме премахнатия ръб (мост), отидете през него стигаме до друг връх, който преди това е имал нечетна степен, и ние предаваме втория компонент на връзката на цикъла на Ойлер. Във всички анализирани случаи получаваме път на Ойлер, който е започнал в един от върховете с нечетна степен и завършил в друг. Теоремата е доказана.

Имайте предвид, че всичките 4 върха на мултиграфа (фиг. 2), съответстващи на мостовете на Кьонигсберг, имат степен 3. Следователно цикъл или път на Ойлер е невъзможен.

Забележка. Ако графика (или мултиграфия без цикли) съдържа 2k върхове с нечетна степен, тогава тя може да бъде разделена на k полу-ойлерови графики (т.е. нарисувайте k с мазки на писалката). Доказателството е подобно на това на теоремата на Ойлер.

Съществува прост алгоритъм (така нареченият алгоритъм на Fleury) за намиране на цикъла на Ойлер (разбира се, ако този цикъл съществува), който се състои в следното: започваме от всеки връх и „изтриваме“ пресечените ръбове. В този случай преминаваме през моста (провлака) само ако няма други възможности.

Очевидно е, че за да се изгради Ойлерова пътека, е достатъчно да се използва алгоритъмът на Fleury, който трябва да започне от връх с нечетна степен.

Нека има някаква графика (свързана), на чиито ръбове се приписват някои числа, наречени тегла на ръбовете (често, но не винаги!, В приложенията теглото на ръба е неговата дължина). Необходимо е да се намери цикъл, така че всеки ръб да бъде преминат поне веднъж и общото тегло на всички ръбове, включени в цикъла, да е минимално. Имайте предвид, че ако графиката е Ойлер, тогава всеки цикъл на Ойлер решава проблема (за графика на Ойлер тежестите не играят роля).

Тази задача има много приложения, например поливане на улици с една кола (тук ръбовете на графиката са пътища, а кръстовищата са върхове; тежестите са дължините на пътищата), както и събирането на боклука, доставката на поща или дори най-добрият маршрут за посещение на музей или почистване на стаи и коридори в големи институции.

Нека да разгледаме накратко проблема, свързан с евентуално обхождане на всички върхове в графика: има ли цикъл (или маршрут) в даден (свързан) граф, който преминава всеки връх (с изключение на първия) само веднъж? Ако такъв цикъл (маршрут) съществува (в този случай такъв цикъл ще бъде контур, а маршрут ще бъде път), тогава графиката се нарича хамилтонов (полу-хамилтонов) и съответният цикъл (път) е наричан още хамилтонов цикъл (пътека).

На фиг. 6 изобразява хамилтонови, полухамилтонови и нехамилтонови графики.

Въпреки сходството на формулировката на задачите за хамилтоновите графове с онелевите, няма „добро“ решение за хамилтоновите графики. Като цяло за хамилтоновите графики се знае много малко. По принцип това са теореми от типа „ако графиката има достатъчен брой ребра, то тя е хамилтонова“. Ясно е, че теоремите от този тип не могат да дадат критерий за хамилтонов граф (фиг. 6, а), тъй като в графики от този тип може да има много върхове и сравнително малко ребра).

Представяме без доказателство най-известната теорема.

Теорема (Дирак, 1952). Ако в свързана графика с n върха (за nі3) градусите на всички върхове са по-големи или равни на n/2, тогава графиката е хамилтонова.