Пакет вектор

Пакет вектор се нарича определена геометрична конструкция, съответстваща на семейство векторни пространства, параметризирани от друго пространство X (например X може да бъде топологично пространство, многообразие или алгебрична структура): всяка точка x от пространството X е свързана с векторно пространство V x > така че техният съюз да образува пространство от същия тип, като X (топологично пространство, многообразие или алгебрична структура и т.н.), наречено пространство на векторно снопче над X . Извиква се самото пространство X основен пакет.

Векторният пакет е специален тип локално тривиални пакети, които от своя страна са специален тип пакети.

Обикновено се разглеждат векторни пространства върху реални или комплексни числа. В този случай се казва, че векторните снопове са съответно реални или сложни. Сложните векторни снопове могат да се считат за реални с допълнително въведена структура.

Най-простият пример е тривиален пакет, който има формата на директно произведение X × V, където X е топологично пространство (основа на пакета), а V е векторно пространство.
По-сложен пример е

Векторен пакет е локално тривиален пакет, чието влакно V е векторно пространство със структурна група от обратими линейни трансформации V .

Подгрупата U векторни снопове V върху топологичното пространствох е колекция от линейни подпространства U x ⊂ V x \ подмножество V_>, x ∈ X, която сама по себе си има структурата на векторния пакет.
Пакет от линии е векторен пакет от ранг 1.

Морфизъм от векторния пакет π 1: E 1 → X 1 \ двоеточие E_ \ до X_> до векторния пакет π 2: E 2 → X 2 \ двоеточие E_ \ до X_> се дава от двойка непрекъснати карти f: E 1 → E 2 \ до E_> и g: X 1 → X 2 \ до X_> такива, че

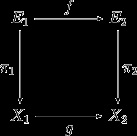
g ∘ π 1 = π 2 ∘ f = \ pi _ \ circ f>
за всеки x ∈ X 1>, отображението π 1 - 1 ( < x >) → π 2 - 1 ( < g ( x ) >), ^ (\) \ to \ pi _ ^ (\),> индуцирано от f, е линейно картографиране на векторни пространства.

Обърнете внимание, че g се дефинира от f (тъй като π 1> е сюррекция), в този случай казваме, че f корици ж .

Нарича се пакет хомоморфизъм от E 1> до E 2>, заедно с обратния хомоморфизъм изоморфизъм на (векторни) снопове. В този случай се извикват сноповете E 1> и E 2> изоморфен. Нарича се изоморфизъм на векторния пакет (от ранг k) E над X върху тривиален пакет (от ранг k над X) банализация E и E се нарича тривиален (или тривиализуем). От дефиницията на векторен пакет става ясно, че всеки векторен пакет локално тривиален.

Повечето операции върху векторни пространства могат да бъдат продължени към векторни пакети, като направите по посока.

Например, ако E е векторен пакет на X, тогава има наречен пакет E ∗> на X конюгиран пакет, чието влакно в точка x ∈ X е двойното векторно пространство (E x) ∗) ^>. Формално E ∗> може да се определи като набор от двойки (x, φ), където x ∈ X и φ ∈ E x ∗ ^>. Свързаният сноп е локално тривиален.

Има много функционални операции, изпълнявани върху двойки векторни пространства (над едно поле). Те се простират директно до двойки векторни снопове E, F на X (над дадено поле). Ето няколко примера.

Уитни сума, или пакет с директна сума E и F е векторно снопче E ⊕ F на X, чието влакно в точката x е пряката сума E x ⊕ F x \ oplus F_> на векторни пространства E x> и F x>.

Свържете продукта на тензора E ⊗ F се дефинира по подобен начин, като се използват точките на тензорни произведения на векторни пространства.

Сноп от хомоморфизми (хом-пакет) Hom (E, F) \, (E, F)> е векторен сноп, чието влакно в точката x е пространството на линейни карти от E x> до F x> (често се означава с Hom (E x, F x ) \, (E_, F _)> или L (E x, F x), F _)>). Този пакет е полезен, тъй като има биекция между хомоморфизмите на векторни снопове от E до F на X и частите Hom (E, F) \, (E, F)> на X .