Велика енциклопедия на нефт и газ

Симетрично произволно ходене

От друга страна, нека разгледаме две частици, които правят независими симетрични произволни разходки и движенията им се извършват едновременно. [16]

В задачи 1.12 - 1.19 се изучават различни свойства на траекториите на симетрично произволно ходене. [17]

Sn - положението на частицата в момент n в симетрично произволно ходене - има разпределение p (A) C. [18]

Оказва се обаче, че в случай на измерение три или повече, симетричното произволно ходене е необратимо. [19]

Оказва се обаче, че в случай на измерение три или повече, симетричното произволно ходене е необратимо. [20]

В този случай всички състояния на системата се повтарят и частицата се връща във всяко от състоянията безкраен брой пъти по време на неограничено продължително симетрично произволно ходене. За система с произволно ходене граничният вектор не съществува, тъй като нито за pq, нито за p/q състоянията на веригата са ергодични. [21]

Вероятностната схема, построена за проблема с руините на играча, също описва симетрично произволно ходене на частица по едномерна решетка с абсорбиращи екрани. Подобна схема понякога се използва, например, за описване на едномерно броуновско движение, при което частица е ударена от голям брой хаотично движещи се молекули. Абсорбиращите екрани са разположени в точките - mvL c - m: ако частица попадне в някоя от тях, тя остава там. [22]

И така, следният резултат е верен (Поля): за пространствата R1 и R симетричното произволно ходене е повтарящо се, а за пространствата I З е необратимо. [23]

И така, следният резултат е верен (Поля): за пространствата R1 и R2 симетричното произволно ходене е повтарящо се, а за пространствата R и & 3 е необратимо. [24]

И така, следният резултат (Polya) е верен: за пространствата R1 и R2 симетричното произволно ходене е повтарящо се, а за пространствата Rn, n 3 е необратимо. [25]

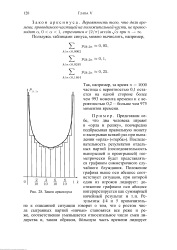
Последователността на резултатите от отделните игри (последователността на победите и загубите) ще бъде геометрично представена от графика на симетрично произволно ходене. [27]

Когато R = 0, стигаме до заключението: вероятността точката y да бъде достигната по-рано от точката O е равна на x/y (точно както в симетричното произволно ходене, съответстващо на схемата на Бернули, вижте проблема с руините в 1; гл. [28]

Помислете за симетрично произволно ходене в ограничена област на равнината.Границата е неправилна в смисъл, че винаги, когато частица трябва да напусне региона в право неограничено произволно ходене, Сиа е принудена да се върне в предишното си положение. Покажете, че ако всяка точка на региона е достъпна от всяка друга точка, тогава има стационарно разпределение и това uk 1/d, където a е броят на държавите в региона. [29]

Помислете за симетрично произволно ходене в ограничена област на равнината. Границата му отразява в смисъл, че всеки път, когато частицата трябва да напусне този регион в неограничено произволно ходене, тя е принудена да се върне в предишното си положение. Покажете, че ако всяка точка на региона е достъпна от която и да е друга точка, тогава има стационарно разпределение и това 1/o, където a е броят на позициите в региона. Ако площта не е ограничена, тогава състоянията са върнати нула и b1 определя инвариантна мярка. [тридесет]