РАЗДЕЛ I. ОПТИМИЗАЦИОННИ МЕТОДИ

1. ОТЧЕТ ЗА ПРОБЛЕМИТЕ ЗА ОПТИМИЗАЦИЯ И КЛАСИФИКАЦИЯТА им.

1.1. Формулиране на проблема

Основната цел на повечето изчисления, извършени на компютър, е да се вземе оптималното решение в конкретна ситуация или, което е същото, да се направи най-добрият избор от множество приемливи опции. Например колко и къде да инвестирате, за да получите най-голяма печалба; по кой път да поемете, за да спестите газ, време и в същото време да осигурите безопасност; как да изберем параметрите на устройството, така че да се постигне максимална ефективност при минималните производствени разходи.

Във всеки случай, когато се решава проблемът на избора, се изисква да се изгради математически модел, описващ конкретна ситуация. Формулировката на модела съдържа определен брой параметри x = < x 1 . x n >, в смисъл като-

rykh съответства на конкретна опция. Резултатът от решаването на съответната математическа задача за дадена стойност на параметрите е стойността на целевата функция f (x), която определя стойността на избраната опция.

Така че за горните примери за ситуации: f 1 (x r) - стойност на печалбата, f 2 (x r) - номер на пътя, f 3 (x r) - стойност на ефективността.

В резултат проблемът с вземането на оптимално решение води до намиране на оптималната (максимална или минимална) стойност f (x). Трябва да се отбележи, че намирането на максимума на f (x) е еквивалентно на намирането

- f (x), така че стандартните програми са проектирани като

правило за намиране на min f (x) .

Евклидово пространство E n

функция f (x)

Казват, че f (x r) има локален минимум в точката x r *, ако има такъв

ε е квартал на точката x *, в който

f (x *) y 2 се изпълнява, след което се присвоява

Ако b-a> 2 ε, тогава повтаряме от т. 1, в противен случай от т. 5.

Изчислете x m = (a + b)/2, y m = f (x m).

Средно за едно изчисление на функцията сегментът, на който се намира х, намалява с около 0,75 пъти. Този метод е лесен за изпълнение, той ви позволява да намерите минимума на прекъсната функция, но изисква голям брой изчисления на функцията, за да се осигури определената точност.

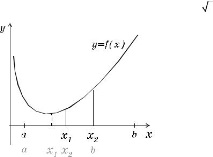
Метод на златното сечение

Златното сечение е разделяне на отсечка a b на две неравни части a

x 1 и x 1 b, при което има следната връзка:

x 1 b/ab = ax 1/x 1 b = 1 - ξ 0,62,

Алгоритъм за намиране на минималния аналог-

подобно на MDP, описано по-горе и различно-

е, че в началото точките x 1 и x 2 са нокаутирани-

така че златното

съотношение и стойностите

функции в тези точки:

Впоследствие, след следващия

скъсяване на интервала чрез изхвърляне-

неблагоприятна екстремна точка, на

останалият сегмент вече има точка,

разделяйки го в златно съотношение, (точно-

ka x 1 на фиг. 1.1) стойността

в този момент. Остава само

изберете симетрично към него и изчислете

стойността на функцията в този момент по ред,

за да решите коя от крайните точки

1.x 1 = a + ξ (b - a), x 2 = b - ξ (b - a), y 1 = f (x 1), y 2 = f (x 2) .

2. Ако y 1> y 2, тогава a = x 1,

x 1 = x 2, y 1 = y 2,

x 2 = b- ξ (b-a); y 2 = f (x 2),

x 2 = x 1, y 2 = y 1,

x 1 = a + ξ (b-a), y 1 = f (x 1).

3. Ако (b-a)> ε, повторете стъпка 2.

4.x m = (a + b)/2, y m = f (x m) .

За едно изчисление на функцията сегментът, на който е разположен x m, намалява с

1- ξ 0,62 пъти, т.е. по-бързо от MDR. Този метод е най-добрата среда-

class di методи 1.

Метод на последователно търсене

Идеята на този метод е, че слизайки от точката x 0 с дадена стъпка h в посока на намаляване на функцията, се установява интервал с дължина h, на който е минимумът, и след това се прецизира. Прецизирането може да се извърши или чрез метода на златното сечение, или чрез повторение на спускането от последната точка, намаляване на стъпката и промяна на нейния знак. Алгоритъмът за последната опция е даден по-долу.

X 0, някаква стъпка h и грешка ε .

1. От точка x 0 се прави стъпка x 1 = x 0 + h и y 1 = f (x 1) .

2.x 0 = x 1, y 0 = y 1 - запомня се успешна точка.

3.x 1 = x 0 + h, y 1 = f (x 1) - направете следващата стъпка в добра посока.

4. Ако функцията намалее, y 1 ε/4, след това повторете от т. 2, в противен случай преминете към т. 7.

7.x m = x 0, f m = f 0, край.

Скоростта на конвергенция на този метод по същество зависи от успешния избор на първоначалното приближение x 0 и стъпката h. Стъпка h трябва да бъде избрана като половината от оценката на разстоянието от x 0 до приетия минимум x m .

Квадратичен метод на парабола

За да се ускори спускането до минимум от някаква точка x 0, се използват локални свойства на функцията в близост до тази точка. По този начин скоростта и посоката на намаляване могат да се определят от величината и знака на първата производна. Втората производна характеризира посоката на изпъкналост: ако f ''> 0, тогава функцията има изпъкналост надолу, в противен случай нагоре. Близо до локален безусловен минимум, двойно диференцируемата функция винаги е изпъкнала надолу. Следователно, ако в близост до минималната точка функцията се апроксимира от квадратна парабола, тогава тя ще има минимум. Това свойство се използва в метода на квадратичната парабола, чиято същност е следната.

Три точки x 1, x 2, x 3 са избрани близо до точката x 0. Изчисляват се стойностите y 1, y 2, y 3. Чрез тези точки се изчертава квадратна парабола