Потапов М

§ 4. Степента на положително число

4.1. Рационална оценка

Решение.
1) 4 a 1,5 - 8 - 0,5 - 2 a + 2 a 0,5 + 4 = 4 a 1,5 - 8 - (a 0,5 - 2) 2 (a 0,5 - 2) (a + 2 a 0,5 + 4) = = 4 a 1,5 - 8 - a - 4 a 0,5 + 4 a 1,5 - 8 = - a + 4 a 0,5 a 1,5 - 8;

2) - a + 4 a 0,5 a 1,5 - 8 ⋅ a 2 - 8 a 0,5 a - 16 = - a 0,5 (a 0,5 - 4) a 0,5 (a 1, 5 - 8) (a 1,5 - 8) (a 0,5 - 4) (а 0,5 + 4) = - аа 0,5 + 4;

3) B = - a a 0.5 + 4 - 4 a 0.5 a 0.5 + 4 = - a 0.5 (a 0.5 + 4) a 0.5 + 4 = - a 0.5 .
Подчертаваме, че всички трансформации на израза B се извършват тук за онези a, за всеки от които всички разглеждани изрази имат смисъл, т.е. .
4.23. а) Може ли стойността на израза A = x 1 1 3 - x 1 3 x 1 3 - x - 2 3 + 0,25 - 1,5 - 9 (x - 2) 0 да е равна на 1?
Решение. Първо, трансформираме израза A, приемайки, че x> 0, x ≠ 1, x ≠ 2, тъй като в противен случай този израз е недефиниран:

A = x 1 3 (x - 1) x - 2 3 (x - 1) + (1 4) - 3 2 - 9 ⋅ 1 = x + 8 - 9 = x - 1 .

Сега нека разберем дали съществува такова x, отговарящо на условията x> 0, x ≠ 1, x ≠ 2, за които

Уравнение (1) има уникален корен x = 2. Това означава, че няма такъв x, който да отговаря на условията x> 0, x ≠ 1, x ≠ 2, за които равенството (1) е вярно. Следователно израз A не може да бъде равен на 1.
Междинен контрол. С-18.

4.3. Концепция за ограничение на последователността

В този параграф първо се въвежда понятието безкрайно малко (последователност или променлива), докато на основното ниво терминът „стремим се“ не е формализиран, достатъчно е да научим учениците да намират правилно безкрайно малко от предложените променливи. В учебника има формално определение за безкрайно малко в езика "ε - N", а също така се въвежда понятието за безкрайно голямо. Те са предназначени за напреднало изучаване на математика. Понятието за ограничение на последователността се формира, използвайки понятието за безкрайно малко.
Имайте предвид, че за някои студентски задачи 4.25 и 4.29 може да изглежда сложно, тъй като те не могат да разделят полином на моном, бином. Трябва да ги посъветваме да представят тези дроби като сбор от дроби.
В дидактически материали (раздел 19), редица примери за концепцията за границата на последователност.

Тъй като n> 0, ние преписваме неравенството (1) във формата

Тъй като n> 0 и ε> 0, неравенството (2) е еквивалентно на неравенството

Тъй като n> 0, неравенството (3) може да бъде пренаписано като

4,4 *. Гранични свойства

Тази клауза дава свойствата на границите на сумата, разликата, произведението и коефициента и свойството да се приема постоянен коефициент отвъд знака на лимита. Доказателствата за тези свойства не са предоставени от програмата и не са дадени в учебника.

Междинен контрол. С-19.

4.5. Безкрайно намаляваща геометрична прогресия

В този параграф припомняме формулата за n-ия член на геометрична прогресия, формулата за сумата от първите n членове. Нека обърнем внимание на особеността на терминологията: не всяка безкрайно намаляваща прогресия е намаляваща прогресия. Ако - 1 q 0, тогава прогресията не намалява, например геометричната прогресия 1, - 1 2, 1 4, - 1 8,. не намалява, но е безкрайно намаляваща прогресия, тъй като q = - 1 2 и | q | един .
Добре известна психологическа трудност е свързана с безкрайно намаляваща прогресия, която учениците трудно могат да преодолеят: буквата S обозначава сумата от безкраен брой членове a + aq + aq 2 + ..., безкраен процес на добавяне не може да бъде попълнено, но сумата съществува и се изчислява по формулата a 1 - q .

Ето два примера, които ще позволят на учениците да се примирят с идеята, че безкраен процес на добавяне може да има краен резултат.
1) Ако дължината на отсечката 1 3 m е изразена като десетична дроб, тогава получаваме 0,3333. m, или 0,3 + 0,03 + 0,003 + 0,0003 +. м.
2) Ако площта на квадрата е равна на 1 и първата половина на квадрата е боядисана, след това половината от небоядисаната част, след това половината от останалата неоцветена част от квадрата и т.н., тогава процесът на боядисване е безкраен, но е очевидно, че „в границата“ площта на запълнената част на квадрата е равна на площта на квадрата, тоест равна на 1. Това се потвърждава и от прилагането на формулата за сумата на безкрайно намаляваща прогресия: 1 2 + 1 2 2 + 1 2 3 +… = 1 2 1 - 1 2 = 1 (вижте задачата 4.38и).

4.40. а) Докажете, че числото 0, (3) е сумата от поредицата 0,3 + 0,03 + 0,003 + . .
Решение. Сумата от безкрайно намаляваща геометрична прогресия 0,3 + 0,03 + 0,003 +. е равен на фракцията 0,3 1 - 0,1 = 1 3, а фракцията 1 3 е равна на безкрайната периодична десетична фракция 0, (3). По този начин сумата от поредицата е 0,3 + 0,03 + 0,003 +. = 0, (3).
Задачи 4.43 и 4.44 са задачи за независими изчисления. Практиката показва, че има малко десетокласници, които могат самостоятелно да очертаят план за решаване на подобни проблеми. Най-често учителят трябва да очертае този план или да реши първия проблем с учениците, надявайки се, че един от тях ще успее да реши втория.
4.43. Страните на квадрата (фиг. 21, а) бяха разделени на 3 равни части. На всеки среден участък във външната зона беше вграден нов квадрат и този среден участък беше премахнат. Резултатът е фигурата, показана на фигура 21, b. След това всяка страна на получената фигура беше разделена на 3 равни части. На всеки среден участък е построен нов квадрат до външната зона и този среден участък е премахнат. Резултатът е фигурата, показана на фигура 21, c. Третата фигура е получена по същия начин (фиг. 21, г) и т.н.

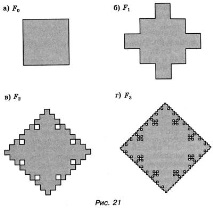
s n = k n ⋅ (a n) 2 = 4 ⋅ 5 n - 1 ⋅ (a 3 n) 2 = 4 9 a 2 ⋅ (5 9) n - 1 .

Сборът от площите на всички нови квадрати, получени при преобразувания от 1-ви до n-ти, е сумата от първите n членове на геометричната прогресия, тя е равна на

s 1 + s 2 + s 3 +… + sn = 4 9 a 2 + 4 9 a 2 ⋅ 5 9 + 4 9 a 2 ⋅ (5 9) 2 + …… + 4 9 a 2 ⋅ (5 9) n - 1 = 4 9 a 2 (1 + 5 9 + (5 9) 2 +… + (5 9) n - 1) = = 4 9 a 2 ⋅ 1 - (5 9) n 1 - 5 9 = a 2 ⋅ (1 - (5 9) n) = a 2 - a 2 ⋅ (5 9) n .

Тогава площта S n на фигурата F n е S n = a 2 + a 2 - a 2 ⋅ (5 9) n, тя има тенденция към 2 + a 2 = 2 a 2 при n → + ∞ .
Отговор. а) S n = 2 a 2 - a 2 ⋅ (5 9) n; б) 2 а 2; в) P n = 4 a ⋅ (5 3) n; г) P n → + ∞ като n → + ∞ .

4.7. Понятието за степен с ирационален показател

4.49. Кои две съседни естествени числа съдържат числото 2 2 ?
Тъй като 1 2 2, след това 2 1 2 2 2 2, т.е. 2 2 2 4. Но дясното неравенство може да бъде по-точно. Тъй като 1.4 2 1.5, след това 2 2 2 1.5. Тъй като 2 1,5 = 2 2 = 2,8 ... 3, тогава 2 2 3 .
Така че 2 2 2 3 .
4.50. Изградете не намаляваща последователност, чиято граница е 2 π (π = 3.1415926 ...) .
Отговор. 2 3, 2 3.1, 2 3.14, 2 3.141, 2 3.1415, ... .
Допълнителен въпросс. Защо конструираната последователност не намалява и не се увеличава строго?
Отговор. Тъй като в някакъв бит от числото π може да има цифра 0, тогава два съседни члена на последователността ще бъдат равни.
4.51. а) Изчислете 2 3 ⋅ 2 2 - 3 .
Решение. Преобразуваме продукта, като използваме свойството 1-ва степен:

2 3 ⋅ 2 2 - 3 = 2 3 + 2 - 3 = 2 2 = 4 .

4.8. Експоненциална функция

Подразделът въвежда функцията y = a x, където a> 0, a ≠ 1, x ∈ R, разглеждат се свойствата на тази функция и нейната графика. Тези свойства ще бъдат използвани допълнително при доказване на свойствата на логаритмичната функция, при решаване на експоненциални уравнения и неравенства.

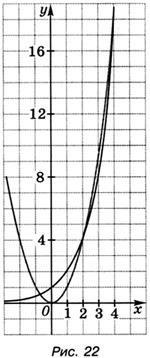
4.59. Определете графично колко корена има уравнението 2 x = x 2 .
Когато решават този проблем, учениците обикновено се ограничават до разглеждане на графиките на функциите в обичайните граници за y ≤ 10 и намират само две точки на пресичане на графиките. И са три (фиг. 22). Следователно уравнението 2 x = x 2 има три корена, единият от които е отрицателен, а другите два са положителни: x = 2 и x = 4 .

Междинен контрол .
Тестова работа номер 3.