Определен интеграл

Лекция 1. Определен интеграл

1. Понятието за определен интеграл

2. Геометрично значение на определен интеграл

3. Основни свойства на определен интеграл

4. Формула на Нютон - Лайбниц

5. Промяна на променлива в определен интеграл

6. Интегриране по части

Лекция 2. Приложение на определени интеграли. неправилни интеграли

1. Площ на извит трапец

2. Обемът на тялото на революцията

3. Дължината на дъгата на плоска крива

4. Неправилни интеграли с безкрайни граници на интеграция

5. Неправилни интеграли на неограничени функции

Лекция 1. Определен интеграл

1. Понятието за определен интеграл

Нека функцията бъде дефинирана на интервала,. Нека извършим следните операции:

1) разделяме сегмента по точки на n частични сегмента;

2) във всеки от частичните сегменти изберете произволна точка и изчислете стойността на функцията в тази точка:;

3) намерете продукта, където е дължината на частичния сегмент,;

4) съставете сумата

, (един)

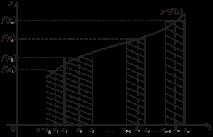
което се нарича интегрална сума на функцията y = f (x) на отсечката [a, b]. От геометрична гледна точка интегралната сума е сумата от площите на правоъгълници, чиито основи са частични сегменти, а височините са равни, съответно (фиг. 1). Нека означим с дължината на най-големия частичен сегмент;

5) намери границата на интегралната сума, когато .

Определение. Ако съществува крайна граница на интегралната сума (1) и тя не зависи от метода за разделяне на сегмент на частични сегменти или от избора на точки в тях, тогава тази граница се нарича определен интеграл на функция на сегментът и е означен .

Поради това, .

В този случай функцията се нарича интегрируема включена. Числата a и b се наричат съответно долната и горната граници на интегриране - интегранда, - интегранда, - променливата на интеграция; сегментът се нарича интервал на интегриране.

Теорема 1. Ако дадена функция е непрекъсната в даден сегмент, то тя е интегрируема в този сегмент.