Концепция за фазово пространство. Метод на фазовата равнина

Страници за работа

Съдържанието на произведението

Лекция 11.Концепция за фазово пространство. Метод на фазовата равнина.

Фазовото пространство или пространството на състоянието на системата е н-размерно пространство, координатите в което са фазови променливи (променливи на състоянието) на системата. Размерът на фазовото пространство съответства на измерението на системата, тоест реда на системата от диференциални уравнения в нормална форма (форма на Коши), описваща дадената система.

В общия случай за нелинейна система такъв модел е:

i =1,2. н, (11.1)

където ji - нелинейни функции; xi - фазови променливи на системата; ж, е- настройка и смущаващи влияния (евентуално векторни функции).

Ако използвате вектор на фазови променливи, можете да напишете този модел във векторна форма:

. (11.2)

Аргумент т в уравнения (11.1) - (11.2) присъства само за нестационарни системи.

IN н-размерно фазово пространство (фиг. 51) до началния момент от времето за процеса в системата т0 съответства на точка, представляваща началното състояние на системата х 0 = (хдесет,х20, ...,xn0). Към всеки следващ момент във времето t> t0 ще съответства на друга точка, чиито координати са текущите стойности на фазовите променливи. Нарича се представителна точка. Решението на уравнения (11.1) - (11.2) xi(т), i =1,2. н, има някаква непрекъсната крива, която се нарича фазова траектория на процеса в системата. Стрелката на фазовата траектория показва посоката на нарастване на времето.

Освен това отбелязваме, че стойностите на дясните страни на уравнения (11.1) дават проекциите на вектора на скоростта на движението на представящата точка по фазовата траектория за всеки разглеждан момент от време.

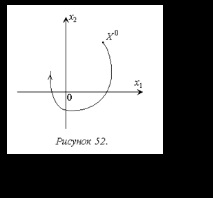
Като правило не е възможно да се използва картографиране на процес в система в многомерно фазово пространство за решаване на практически проблеми. Следователно най-честото използване на разглеждания апарат е методът на фазовата равнина, когато се вземат предвид само две променливи от състоянието на системата и фазовите траектории са плоски криви (фиг. 52). Очевидно методът на фазовата равнина позволява да се получи пълна картина на процеса само за системи от втори ред. За такива системи се използва главно.

В повечето случаи, когато се използва методът на фазовата равнина, входните сигнали ж и е вземете равно на нула и разгледайте процесите, причинени от първоначалните отклонения на фазовите променливи от стационарните стойности. За стационарна система от втори ред, системата от уравнения (11.1) ще приеме формата:

. (11.3)

Полученият набор от фазови траектории за различни начални условия се нарича фазов портрет на системата.

Имайте предвид, че когато се използва математически модел на системата, физическото значение на фазовите променливи не се взема предвид. Следователно, дори за система от втори ред, различни двойки (хедин, х2) със съответни промени на променливи в уравнения (11.3). Изборът на фазови променливи се извършва в зависимост от проблема, който трябва да бъде решен, за удобство на неговото решение.

Най-често срещаният избор на фазови променливи предвижда пряка връзка между тях от следната форма. Тогава уравненията (11.3) са опростени:

. (11.4)

Удобството на такъв модел при използване на метода на фазовата равнина се определя от факта, че за него вертикалната координата е производна на хоризонталната. В резултат на това фазовите траектории се подчиняват на следните правила:

1. В горната полуплоскост движението на представителната точка по фазовата траектория е възможно само отляво надясно, в долната половина - само в обратната посока.

Това правило се обяснява с факта, че за горната полуплоскост, тоест когато тук е намерена представителната точка, нейната хоризонтална координата непременно се увеличава. За долната полуплоскост е обратното.

2. Фазовите траектории пресичат хоризонталната ос само под прав ъгъл.

В точките на пресичане с хоризонталната ос, тоест, когато оста е пресечена, хоризонталната координата на представящата точка не се променя и допирателната към фазовата траектория е насочена вертикално.

3. Фазовите пътеки не могат да се пресичат.

Това правило е валидно за системи от втори ред за всеки избор на фазови променливи, освен ако уравненията на системата съдържат променливи във времето входни сигнали. Във всеки случай той е валиден за модели от формата (11.3) - (11.4), които за всяка точка във фазовото пространство дават уникални стойности на компонентите на вектора на скоростта на представящата точка.

Нека разгледаме някои примери, които демонстрират връзката между фазовите траектории и времевите характеристики и метод, базиран на него, за изграждане на фазови траектории.

За трептяща връзка с трансферна функция

при липса на входен сигнал, равновесното състояние е стабилно и съвпада с началото, докато преходният процес се възбужда от началните условия за изходния сигнал и неговата производна, които обозначаваме съответно, х1 и х2. Закони за промяна х1 и х2 са показани на фиг. 53и. Точките, съответстващи на екстремумите и нулите на разглежданите функции, се нанасят на техните графики. Съответните точки са основата за изграждане на фазова траектория на равнина с координати х1 и х2 (фиг. 53б).

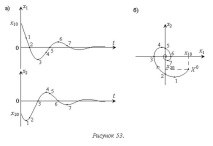
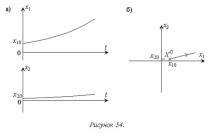
По-долу има подобна конструкция за нестабилна апериодична връзка с трансферна функция .

Изходният сигнал на връзката се избира като фазови координати х1 и производната му. При липса на входен сигнал се разглежда процес, иницииран от първоначалните условия. Диференциалното уравнение на връзката ще има формата:

Неговото решение: Tp-1 = 0, .

Законът за промяна на производната се получава чрез диференциране:

По този начин вертикалната координата на началната точка за фазовата траектория е:, а уравнението на фазовата траектория е уравнението на права линия, преминаваща през началото:. Фазовата траектория е показана на Фигура 54.

Да се върнем към системата от уравнения (11.3). Равновесните състояния на системата съответстват на постоянството на фазовите променливи, т.е. изчезването на техните производни. За линейна система е възможно само едно състояние на равновесие. Нелинейната система може да има няколко от тях. Всяко равновесно състояние отговаря на някаква точка на фазовата равнина.

Въз основа на (11.3) може да се получи единно диференциално уравнение на фазовата траектория:

. (11,5)

Дясната му част дава ъгъла на наклон на допирателната към фазовата траектория, тоест посоката на вектора на скоростта на представящата точка. Това важи за всяка точка във фазовата равнина, с изключение на точки, съответстващи на равновесни състояния. За тях дясната страна на уравненията (11.3) изчезва и несигурността възниква от дясната страна на уравнението (11.5). Следователно такива точки се наричат единични точки на фазовата равнина.

Горният метод за изграждане на фазови траектории изисква получаване на законите за промяна на фазовите променливи хедин (т) и х2 (т). Това се постига чрез решаване на системи от уравнения от вида (11.4) или (11.5). За нелинейните системи тук в повечето случаи се изисква използването на приблизителни числени методи. В този случай изграждането на фазовия портрет на системата е свързано с множество решения на уравненията.

Поради това често е по-удобно да се анализират единични точки и единични линии на фазовата равнина, което дава възможност да се получи доста пълна картина на фазовия портрет и отразяваните от него свойства на системата.