Числа на Фибоначи - Формула на Бине - Идентичности - Свойства - Вариации и обобщения
Числа на Фибоначи
Числа Фибоначи - елементи от числова последователност
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 ... (последователност A000045 в OEIS)
при което всяко следващо число е равно на сумата от двете предходни числа. Кръстен на средновековния математик Леонардо от Пиза (или Фибоначи).
По-формално, последователността на числата на Фибоначи се дава от връзката на повтаряемостта:
Понякога числата на Фибоначи се разглеждат и за неположителни числа n като двустранна безкрайна последователност, която удовлетворява основната връзка. Членовете с такива числа могат лесно да бъдат получени с помощта на еквивалентната обратна формула: Fn = Fn + 2 - Fn + 1:
н
Лесно е да се види, че F - n = (- 1) n + 1 Fn. Повечето от следните свойства остават валидни за числата на Фибоначи с отрицателни индекси.
Формулата на Бине
Формулата на Бине Изрично изразява стойността на Fn като функция от n:
,
където е златното сечение. Освен това те са корените на квадратното уравнение .
От формулата на Бине следва, че за всички Fn е най-близо до цяло число, т.е. По-специално асимптотиката .
Самоличности
- Числата на Фибоначи са представени от стойностите на континуантите на набор от единици:, т.е.

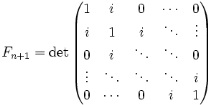
където матриците имат размер, i е въображаемата единица.
- Числата на Фибоначи могат да бъдат изразени чрез полиноми на Чебишев:
- Последствие. Изчисляването на детерминанти дава
Имоти
- Най-големият общ делител на две числа на Фибоначи е равен на числото на Фибоначи с индекса, равен на най-големия общ делител на индексите, т.е. (Fm, Fn) = F (m, n). Последствия:
- Fm се дели на Fn тогава и само ако m се дели на n (с изключение на n = 2). По-специално, Fm се дели на F3 = 2 (т.е. е четно) само за m = 3k; Fm се дели на F4 = 3 само за m = 4k; Fm се дели на F5 = 5 само за m = 5k и т.н.
- Fm може да бъде просто само за просто m (с единственото изключение m = 4) (например 233 е просто и неговият индекс, равен на 13, също е прост). Обратното не е вярно, първият контрапример е. Не е известно дали множеството от числа на Фибоначи, които са прости, е безкрайно.
- Последователността на числата на Фибоначи е частен случай на повтаряща се последователност, нейният характерен полином x 2 - x - 1 има корени и .
- Съотношенията са подходящи фракции от златното съотношение φ и по-специално, .
- Сумите на биномиалните коефициенти върху диагоналите на триъгълника на Паскал са числа на Фибоначи поради формулата
.
- През 1964 г. JHE Cohn доказа, че единствените точни квадрати сред числата на Фибоначи са числата на Фибоначи с индекси 0, 1, 2, 12: F0 = 0 2 = 0, F1 = 1 2 = 1, F2 = 1 2 = 1, F12 = 12 2 = 144. Освен това за n = 0,1,12 твърдението Fn = n 2 .
- Генериращата функция на последователността на Фибоначи е:
- Множеството от числа на Фибоначи съвпада с множеството положителни стойности на полинома
z (x, y) = 2xy 4 + x 2 y 3 - 2x 3 y 2 - y 5 - x 4 y + 2y,
върху множеството неотрицателни цели числа x и y.
- Продуктът и коефициентът на произволни две различни числа на Фибоначи, различни от едно, никога не е число на Фибоначи.
- Последните цифри на числата на Фибоначи образуват периодична последователност с период 60, последната двойка цифри на числата на Фибоначи образуват последователност с период 300, последните три цифри - с период 1500, последните четири - с период от 15000, последните пет - с период от 150 000 и т.н.
Вариации и обобщения
- Числа на Трибоначи
- Числата на Фибоначи са частен случай на последователностите на Лукас, докато тяхното допълнение са числата на Лукас .
- Формулата на Бине е
- ПЕРФЕКТЕН НОМЕР превод от руски на английски, превод от руски на английски
- Титаниева гривна Tianshi информация, свойства, инструкции за употреба
- Тълкуване на сънищата по дни от седмици и дни от месеца
- ПЕРФЕКТЕН НОМЕР