Вершина, свързаност на ръба, връзка между тях и минималната степен на върха

Нека минималната степен на върха на графиката [math] G [/ math] се обозначава с буквата [math] \ delta [/ math]. Тогава:

Нека проверим второто неравенство. Ако графиката [math] G [/ math] няма ръбове, тогава [math] \ lambda = 0 [/ math]. Ако има ребра, тогава получаваме несвързана графика от дадената, премахвайки всички ребра, падащи на върха с най-малка степен. Както и да е [math] \ lambda \ leqslant \ delta [/ math] .
За да проверим първото неравенство, трябва да разгледаме няколко случая.
1. Ако [math] G [/ math] е несвързана или тривиална графика, тогава [math] \ kappa = \ lambda = 0 [/ math] .
2. Ако [math] G [/ math] е свързан и има мост [math] x [/ math], тогава [math] \ lambda = 1 [/ math]. В последния случай, [math] \ kappa = 1 [/ math], защото или графиката [math] G [/ math] има съвместна точка, падаща на ръба [math] x [/ math], или [math] G = K_2 [/ математика] .
3. И накрая, да предположим, че графиката [math] G [/ math] съдържа набор от ръбове [math] \ lambda \ geqslant 2 [/ math], премахването на което я прави прекъсната. Ясно е, че изтривайки [math] \ lambda - 1 [/ math] ръбове от този набор, получаваме графика с мост [math] x = uv [/ math]. За всеки от тези [math] \ lambda - 1 [/ math] ръбове изберете всеки връх, инцидентен с него, различен от [math] u [/ math] и [math] v [/ math]. Премахването на избраните върхове премахва [math] \ lambda - 1 [/ math] (и вероятно повече) ръбове. Ако получената след такова изтриване графика не е свързана, тогава [math] \ kappa \ lt \ lambda [/ math]; ако е свързан, тогава има мост [math] x [/ math] и следователно премахването на върха [math] u [/ math] или [math] v [/ math] води или до несвързана, или до тривиална графика . Както и да е [math] \ kappa \ leqslant \ lambda [/ math] .

Да разгледаме графиката [math] G [/ math], която представлява обединението на две пълни графики [math] G_1 [/ math] и [math] G_2 [/ math], съдържащи върха [math] c + 1 [/ math] . Забележете [math] b [/ math] върхове, принадлежащи на подграф [math] G_1 [/ math] и [math] a [/ math] върхове, принадлежащи на подграф [math] G_2 [/ math]. Добавете ръбове към графиката [math] G [/ math] [math] b [/ math], така че всеки ръб да бъде случайно маркиран с връх, лежащ в подграф [math] G_1 [/ math] и маркиран връх, лежащ в подграф [math] G_2 [/ math] и няма нито един маркиран връх, който да няма поне един нов инцидент на ръба. Тогава:

Тъй като [math] b \ leqslant c [/ math], имаше поне два немаркирани върха, следователно [math] \ delta = c [/ math], тъй като минималните градусови градуси на графиките [math] G_1 [/ math] и [math] G_2 [/ math] бяха равни на [math] c [/ math] и градусите на техните върхове не намаляваха.
Обърнете внимание, че между два върха на графиката [math] G [/ math] има най-малко [math] a [/ math] върхове, несвързани прости пътища, следователно, според теоремата на Менгер, [math] \ kappa \ geqslant a [/ математика]. Ако обаче премахнем от графиката [math] G [/ math] обозначените върхове на нейния подграф [math] G_2 [/ math], тогава графиката [math] G [/ math] ще загуби свързаност. Следователно, [math] \ kappa = a [/ math] .
Подобно на разсъжденията в точка 2, лесно е да се уверите, че [math] \ lambda = b [/ math] .

За да намерите свързаност на ръба, трябва да извършите итерация по всички двойки върхове [math] s [/ math] и [math] t [/ math], да намерите броя на несвързаните пътеки от [math] s [/ math] до [math ] t [/ math] и изберете минимум. Нека е равно на [math] l [/ math]. Според изявлението графиката е свързана с [math] l [/ math] и такъв [math] l [/ math] е максималният (в края на краищата ясно сме намерили броя на пътищата). И така, по дефиниция свързването на ръба е равно на [math] l [/ math] .

За да намерим броя на несвързаните пътища от [math] s [/ math] до [math] t [/ math], използваме алгоритъма за намиране на максималния поток. Съпоставете всеки ръб с капацитет, равен на [math] 1 [/ math] и намерете максималния поток (например алгоритъма на Edmonds-Karp). Тя ще бъде равна на броя на пътеките. В действителност, ако разложим потока, ще получим набор от несъединяващи се краища от [math] s [/ math] до [math] t [/ math], по които потокът е неотрицателен и равен на [math] 1 [/ math] (тъй като. Честотната лента на всички ръбове е [math] 1 [/ math]). Така че, ако потокът е равен на [math] поток [/ math], тогава броят на пътеките е равен на [math] поток [/ math] .

Времето за изпълнение е [math] V ^ 2 \ пъти O (find \ _max \ _flow) [/ math]. Когато се използва алгоритъмът на Едмъндс-Карп, времето е [math] V ^ 2 \ по O (V E ^ 2) [/ math] или [math] O (V ^ 3 E ^ 2) [/ math]

Използвайки подобни изявления и дефиниции за връзката на върховете, стигаме до един и същ алгоритъм с тази разлика, че ще е необходимо да се търсят върхово-несъединени пътища. Можете да ги търсите по същия начин, ако присвоите на всеки връх честотната лента, равна на [math] 1 [/ math]. За целта ще използваме добре познат трик:

Нека разделим всеки връх [math] v [/ math] на графиката на два върха [math] v_1 [/ math] и [math] v_2 [/ math]. Всички ръбове, влезли в [math] v [/ math], ще влязат в [math] v_1 [/ math]. Всички ръбове, излезли от [math] v [/ math], ще излязат от [math] v_2 [/ math]. Също така добавете ръба [math] (v_1, v_2) [/ math] с честотната лента [math] 1 [/ math] .

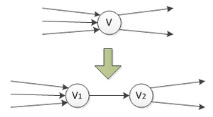
След това, за да намерим броя на пресечните пътища на върховете в оригиналната графика, ще потърсим броя на пресечените пътища на ръба в новата графика.

По този начин, намаляването на проблема до намирането на крайната връзка.