Урок "Пресичане и обединяване на множества"

Раздели: Математика

Цели на урока:

образователни: формиране на умения за идентифициране на набори, подмножества; формирането на умения за намиране на областта на пресичане и обединяване на множества в изображения и именуване на елементи от тази област, решаване на проблеми;
развиване: развитие на познавателния интерес на учениците; развитие на интелектуалната сфера на индивида, развитие на умения за сравняване и обобщаване.
образователни: за възпитаване на точност и внимание при вземане на решение.

По време на занятията.

1. Организационен момент.

2. Учителят комуникира темата на урока, заедно с учениците формулира цели и задачи.

3. Учителят, заедно с учениците, припомня изучения материал по темата „Комплекти“ в 7 клас, въвежда нови понятия и определения, формули за решаване на задачи.

"Много са много, което ние смятаме за един" (основател на теорията на множествата - Георг Кантор). Кантор Георг (1845-1918) - немски математик, логик, богослов, създател на теорията за трансфинитни (безкрайни) множества, оказали решаващо влияние върху развитието на математическите науки в началото на 19 и 20 век.

Множеството е една от основните концепции на съвременната математика, използвана в почти всички нейни раздели.

За съжаление на основната концепция на теорията - концепцията за множество - не може да се даде строга дефиниция. Разбира се, можем да кажем, че даден набор е "колекция", "колекция", "ансамбъл", "колекция", "семейство", "система", "клас" и др. Всичко това обаче не би било математическо определение, а по-скоро злоупотреба с богатството на речника на руския език.

За да се дефинира каквато и да е концепция, на първо място е необходимо да се посочи конкретен случай на това какво по-общо понятие е, за концепцията на множество е невъзможно да се направи това, тъй като няма по-общо понятие от зададени в математиката.

Често трябва да говорим за няколко неща, обединени от определена характеристика. И така, можем да говорим за набора от всички столове в стаята, за набора от всички клетки на човешкото тяло, за набора от всички картофи в дадена торба, за набора от всички риби в океана, за набор от всички квадрати в равнината, за множеството от всички точки на даден кръг и т.н.

Елементите, съставляващи даден набор, се наричат негови елементи.

Например, набор от дни от седмицата се състои от елементите: понеделник, вторник, сряда, четвъртък, петък, събота, неделя.

Много аритметични операции - от елементи: събиране, изваждане, умножение, деление.

Например, ако A означава съвкупността от всички естествени числа, тогава 6 принадлежи на A, а 3 не принадлежи на A.

Ако даден набор съдържа краен брой елементи, то той се нарича краен и ако в него има безкрайно много елементи, тогава той се нарича безкраен. Така че множеството дървета в гората са крайни, а множеството точки на окръжността са безкрайни.

Парадокс в логиката - това е противоречие, което има статут на логично правилно заключение и в същото време е мотивиране, водещо до взаимно изключващи се заключения.

Както споменахме, концепцията за множество е в основата на математиката. Използвайки най-простите множества и различни математически конструкции, можете да конструирате почти всеки математически обект. Идеята за конструиране на цялата математика въз основа на теория на множествата беше активно популяризирана от Г. Кантор. Въпреки цялата си простота, концепцията за набор е изпълнена с опасност от противоречия или, както се казва, парадокси. Появата на парадокси се дължи на факта, че не всички конструкции и не всички множества могат да бъдат разгледани.

Най-простият от парадоксите е "бръснарски парадокс".

На един войник беше наредено да обръсне онези и само онези войници от неговия взвод, които не се бръснат сами. Неизпълнението на заповед в армията е, както знаете, най-тежкото престъпление. Възникна обаче въпросът дали този войник трябва да се обръсне. Ако се бръсне, тогава той трябва да бъде приписан на многото войници, които се бръснат и той няма право да бръсне такива. Ако не се обръсне, той ще попадне в много войници, които не се бръснат и такива войници, според заповедта, е длъжен да се обръсне. Парадокс.

На множества, както и на много други математически обекти, можете да извършвате различни операции, които понякога се наричат теоретични операции на множества или операции на множества. В резултат на операциите се получават нови набори от оригиналните набори. Наборите са обозначени с главни латински букви, а елементите им са обозначени с малки букви. Нотацията aR означава, че елементът a принадлежи към множеството R, тоест a е елемент от множеството R. В противен случай, когато a не принадлежи към множеството R, напишете aR .

Извикват се двата множества A и B равен (A = B) ако се състоят от едни и същи елементи, т.е. всеки елемент от множеството A е елемент от множеството B и обратно, всеки елемент от множеството B е елемент от множеството A .

Сравнение на комплекти.

Набор A се съдържа в набор B (набор B включва набор A), ако всеки елемент от A е елемент на B:

Казват, че набор А се съдържа в набор В или набор А е подмножество множество B (в този случай напишете AB), ако всеки елемент от множеството A е едновременно елемент от множеството B. Тази връзка между множествата се нарича включително. За всеки набор A се извършват следните включвания: ША и А А

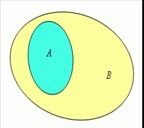
В този случай се извиква A подмножество B, B - супермножество А. Ако, тогава се извиква A собствено подмножество Б. Имайте предвид, че,

A-priory,

Извикват се двата комплекта равен, ако са подмножества помежду си

Задайте операции

Пресичане.

Съюз.

Имоти.

1 Операцията на обединение на множества е комутативна

2. Операцията на обединение на множества е преходна

3. Празният набор X е неутрален елемент от операцията за обединяване на множества

1. Нека A =, B =. Тогава

2. A =, B =. Нека намерим обединението и пресечната точка на тези множества:

, = .

3. Много деца са подгрупа от цялото население

4. Пресичането на множеството от цели числа с множеството положителни числа е множеството от естествени числа.

5. Обединението на множеството рационални числа с множеството ирационални числа е множеството положителни числа.

6. Нула е допълнение към множеството от естествени числа по отношение на множеството от неотрицателни цели числа.

Диаграми на Вен (Диаграми на Вен) - общото наименование на редица методи за визуализация и методи на графична илюстрация, широко използвани в различни области на науката и математиката: теория на множествата, самата "диаграма на Вен", показва всички възможни връзки между множества или събития от определено семейство; разновидности на диаграмите на Вен са: диаграми на Ойлер,

Диаграма на Вен от четири комплекта.

Всъщност "диаграмата на Вен" показва всички възможни връзки между набори или събития от определено семейство. Типична диаграма на Вен има три набора. Самият Вен се опита да намери спретнат начин със симетрични форми, за да представи повече набори в диаграмата, но успя да направи това само за четири набора (вижте фигурата вдясно), използвайки елипси.

Диаграми на Ойлер

Диаграмите на Ойлер са подобни на диаграмите на Вен. Диаграмите на Ойлер могат да се използват за оценка на вероятността от теоретично множествени идентичности.

Задача 1. В класа има 30 души, всеки от които пее или танцува. Известно е, че 17 души пеят, а 19 души знаят как да танцуват. Колко хора пеят и танцуват едновременно?

Решение: Първо, обърнете внимание, че от 30 души 30 - 17 = 13 души не могат да пеят.

Всички знаят как да танцуват, защото по споразумение всеки член на класа пее или танцува. Общо 19 души могат да танцуват, 13 от тях не могат да пеят, което означава, че 19-13 = 6 души могат да танцуват и пеят едновременно.

Проблеми с пресичането и обединението.