Спомагателен ъглов метод в тригонометрични уравнения

В уроците по алгебра учителите ни казват, че има малък (всъщност много голям) клас тригонометрични уравнения, които не могат да бъдат решени с помощта на стандартни методи - нито чрез факторизация, нито чрез променлива промяна, нито дори чрез хомогенни термини. В този случай влиза в действие принципно различен подход - методът на спомагателния ъгъл.

Какъв е този метод и как да го приложим? Като начало припомнете формулите за синуса на сумата/разликата и косинуса на сумата/разликата:

\ [\ begin & \ sin \ ляво (\ alpha \ pm \ beta \ right] = \ sin \ alpha \ cos \ beta \ pm \ cos \ alpha \ sin \ beta \\ & \ cos \ ляво (\ alpha \ pm \ бета \ вдясно) = \ cos \ alpha \ cos \ beta \ mp \ sin \ alpha \ sin \ beta \\\ край \]

Мисля, че тези формули са ви добре известни - от тях се извличат формули на двоен аргумент, без които в тригонометрията като цяло няма никъде. Но нека сега разгледаме просто уравнение:

Нека разделим двете части на 5:

Имайте предвид, че $ \ right)> ^> + \ right)> ^> = 1 $, което означава, че има задължително ъгъл $ \ alpha $, за който тези числа са съответно косинус и синус. Следователно нашето уравнение ще бъде пренаписано, както следва:

\ [\ begin & \ cos \ alpha \ sin x + \ sin \ alpha \ cos x = 1 \\ & \ sin \ ляво (\ alpha + x \ дясно) = 1 \\\ край \]

Днес ще анализираме решението на тригонометрични уравнения, или по-скоро една-единствена техника, която се нарича "спомагателен ъглов метод". Защо точно този метод? Просто защото през последните два или три дни, когато учех със студенти, на които разказвах за решаването на тригонометрични уравнения, и анализирахме, наред с други неща, спомагателния ъглов метод и всички ученици като един допуснаха една и съща грешка. Но методът обикновено е прост и освен това е една от основните техники в тригонометрията. Следователно много тригонометрични задачи изобщо не се решават, освен чрез метода на спомагателния ъгъл.

Затова сега, за начало, ще разгледаме няколко прости задачи, а след това ще преминем към по-сериозни задачи. Въпреки това, всички тези, по един или друг начин, ще изискват от нас да използваме спомагателния ъглов метод, чиято същност ще ви кажа още в първата конструкция.

Решаване на прости тригонометрични задачи

\ [\ cos 2x = \ sqrt \ sin 2x-1 \]

Нека трансформираме малко израза си:

\ [\ cos 2x- \ sqrt \ sin 2x = -1 \ ляво | \ ляво (-1 \ дясно) \ дясно. \]

\ [\ sqrt \ cdot \ sin 2x- \ cos 2x = 1 \]

Как ще го решим? Стандартният трик е да разширите $ \ sin 2x $ и $ \ cos 2x $ с помощта на формули с двоен ъгъл и след това да пренапишете единицата като $ ^> x ^> x $, да получите хомогенно уравнение, да го намалите до допирателни и да решите. Това обаче е дълъг и досаден път, който изисква много изчисления.

Предлагам да помислим върху следното. Имаме $ \ sin $ и $ \ cos $. Припомнете си формулата за косинус и синус на сумата и разликата:

\ [\ sin \ ляво (\ alpha \ pm \ beta \ дясно) = \ sin \ alpha \ cos \ beta \ pm \ cos \ alpha \ sin \ beta \]

\ [\ cos \ ляво (\ alpha + \ beta \ дясно) = \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta \]

\ [\ cos \ ляво (\ alpha - \ beta \ дясно) = \ cos a \ cos \ beta + \ sin \ alpha \ sin \ beta \]

Да се върнем към нашия пример. Нека да намалим всичко до синуса на разликата. Но първо уравнението трябва да бъде леко трансформирано. Нека намерим коефициента:

$ \ sqrt $ е един и същ коефициент, с който двете страни на уравнението трябва да бъдат разделени, така че числата да се появяват пред синуса и косинуса, които сами по себе си са синуси и косинуси. Нека се разделим:

Нека да разгледаме какво имаме вляво: има ли такива $ \ sin $ и $ \ cos $ такива, че $ \ cos \ alpha = \ frac> $ и $ \ sin \ alpha = \ frac $? Очевидно има: $ \ alpha = \ frac \! \! \ Pi \! \! \ Text< >> $. Следователно можем да пренапишем израза си по следния начин:

Сега имаме формулата за синуса на разликата. Можем да напишем така:

Пред нас е най-простата класическа тригонометрична конструкция. Позволете ми да ви напомня:

Нека запишем това за нашия конкретен израз:

Нюанси на решението

И така, какво да направите, ако попаднете на подобен пример:

Преобразувайте структурата, ако е необходимо.
Намерете корекционния коефициент, вземете корена от него и разделете двете части на примера от него.
Вижте какви стойности на синус и косинус се получават от числата.
Разширяваме уравнението според формулите на синуса или косинуса на разликата или сумата.
Решаване на най-простото тригонометрично уравнение.

В това отношение внимателните ученици вероятно ще имат два въпроса.

Какво ни пречи да напишем $ \ sin $ и $ \ cos $ на етапа на намиране на корекционния фактор? - Ние сме възпрепятствани от основната тригонометрична идентичност. Факт е, че получените $ \ sin $ и $ \ cos $, както всеки друг със същия аргумент, трябва да дадат точно "едно", когато е на квадрат. В процеса на решаване трябва да бъдете много внимателни и да не губите „двойка“ преди „xes“.

Методът на спомагателния ъгъл е инструмент, който помага да се намали "грозното" уравнение до напълно адекватно и "красиво".

Виждаме, че имаме $ ^> x $, така че нека използваме изчисления за експоненциално намаляване. Преди да ги използваме обаче, нека ги изведем. За да направите това, не забравяйте как да намерите косинуса на двоен ъгъл:

Ако напишем $ \ cos 2x $ в третата версия, получаваме:

Ще напиша отделно:

Същото може да се направи за $ ^> x $:

Трябват ни само първите изчисления. Нека се заемем с работата по проблема:

\ [\ sqrt \ cdot \ sin 2x + 2 \ cdot \ frac-1 = 2 \ cos x \]

\ [\ sqrt \ cdot \ sin 2x + 1- \ cos 2x-1 = 2 \ cos x \]

\ [\ sqrt \ cdot \ sin 2x- \ cos 2x = 2 \ cos x \]

Сега ще използваме изчисленията на косинуса на разликата. Но първо, нека изчислим корекцията от $ l $:

Нека препишем с този факт предвид:

\ [\ frac> \ cdot \ sin 2x- \ frac \ cdot \ cos 2x = \ cos x \]

В този случай можем да напишем, че $ \ frac> = \ frac \! \! \ Pi \! \! \ Text< >> $ и $ \ frac = \ cos \ frac \! \! \ pi \! \! \ текст< >> $. Нека пренапишем:

Нека сложим минуса в скобата по един умен начин. За целта обърнете внимание на следното:

Връщаме се към нашия израз и помним, че в ролята на $ \ varphi $ имаме израза $ - \ frac \! \! \ Pi \! \! \ Text< >> + 2х $. Затова пишем:

За да разрешите подобен проблем, трябва да запомните това:

\ [\ cos \ alpha = \ cos \ beta \]

\ [\ вляво [\ begin & \ alpha = \ beta +2 \ text< >\! \! \ pi \! \! \ текст< >n \\ & \ alpha = - \ beta +2 \ text< >\! \! \ pi \! \! \ текст< >n \\\ край \ вдясно. \]

Нека да се справим с нашия пример:

Нека изчислим всяко от тези уравнения:

Нека запишем окончателния отговор:

Нюанси на решението

Всъщност този израз е решен по много различни начини, но в този случай оптимален е методът на спомагателния ъгъл. Освен това, използвайки този дизайн като пример, бих искал да насоча вниманието ви към още няколко интересни техники и факти:

Формули за намаляване на степента. Тези формули не трябва да се запомнят, но трябва да знаете как да ги извлечете, което ви казах днес.
Решаване на уравнения от вида $ \ cos \ alpha = \ cos \ beta $.
Добавяне на "нула".

Но това не е всичко. Досега $ \ sin $ и $ \ cos $, които отпечатахме като допълнителен аргумент, предполагахме, че те трябва да са положителни. Затова сега ще решаваме по-сложни проблеми.

Разбор на по-сложни проблеми

Преобразуваме първия член:

\ [\ sin 3x = \ sin \ ляво (2x + x \ дясно) = \ sin 2x \ cdot \ cos x + \ cos 2x \ cdot \ sin x \]

\ [= 2 \ ляво (1- \ cos 2x \ дясно) \ cdot \ sin x \]

Сега нека заместим всичко това в нашата оригинална конструкция:

\ [\ sin 2x \ cos x + \ cos 2x \ sin x + 2 \ sin x-2 \ cos x \ sin x + 4 \ cos x = 5 \]

\ [\ sin 2x \ cos x- \ operatorname-cos2 \ sin x + 2 \ sin x + 4 \ cos x = 5 \]

\ [\ sin \ ляво (2x-x \ дясно) +2 \ sin x + 4 \ cos x = 5 \]

Нека представим нашето изменение:

Такива $ \ alpha $, за които $ \ sin $ или $ \ cos $ ще бъдат равни на $ \ frac $ и $ \ frac $ в тригонометричната таблица. Затова нека просто напишем и намалим израза до синуса на сумата:

\ [\ sin x \ cdot \ cos \ varphi + \ cos x \ cdot \ sin \ varphi = 1 \]

\ [\ sin \ ляво (x + \ varphi \ дясно) = 1 \]

Това е специален случай, най-простата тригонометрична конструкция:

Остава да открием на какво е равен $ \ varphi $. Тук много ученици се объркват. Факт е, че на $ \ varphi $ се налагат две изисквания:

Нека нарисуваме радар и да видим къде се намират такива стойности:

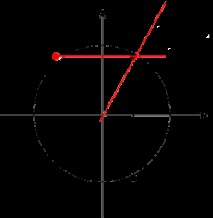
Връщайки се към нашия израз, ще напишем следното:

Но този запис може да бъде оптимизиран малко. Тъй като знаем следното:

тогава в нашия случай може да се напише така:

Това ще изисква още по-задълбочено разбиране на методите за решаване на стандартни задачи без тригонометрия. Но за да разрешим този пример, ние също използваме метода на строителния ъгъл. \ [\]

\ [5 + 2 \ sin 2x-5 \ cos x = 5 \ sin x \]

Първото нещо, което привлича вниманието ви, е, че няма градуси по-високи от първата и следователно нищо не може да бъде разложено от формулите за разширяване на градусите. Ще използва обратни изчисления:

\ [5 + 4 \ sin x \ cos x-5 \ cos x-5 \ sin x = 0 \]

\ [3 + 2 + 4 \ sin x \ cos x-5 \ ляво (\ sin x + \ cos x \ дясно) = 0 \]

Защо разпространих $ 5 $. Вижте тук:

\ [3 + 2 \ ляво (1 + 2 \ sin x \ cos x \ дясно) -5 \ ляво (\ sin x \ cos x \ дясно) = 0 \]

Можем да запишем единицата според основната тригонометрична идентичност като $ ^> x + ^> x $:

\ [3 + 2 \ ляво (^> x + 2 \ sin x \ cos x + co ^> x \ дясно) -5 \ ляво (\ sin x + \ cos x \ дясно) = 0 \]

Какво ни дава такъв запис? Въпросът е, че първата скоба съдържа точен квадрат. Нека да го свием и да получим:

Предлагам да въведете нова променлива:

В този случай получаваме израза:

Общо получаваме:

\ [\ ляво [\ начало & \ sin x + \ cos x = \ frac \\ & \ sin x + \ cos x = 1 \\\ край \ вдясно. \]

Разбира се, знаещите ученици сега ще кажат, че подобни конструкции се решават лесно, като се намалят до еднородни. Ние обаче ще решим всяко уравнение, като използваме метода на спомагателния ъгъл. За целта първо изчисляваме корекцията $ l $:

Нека да разделим всичко на $ \ sqrt $:

Нека да намалим всичко до $ \ cos $:

Справяне с всеки от тези изрази.

Първото уравнение няма корени и ирационалността в знаменателя ще ни помогне да докажем този факт. Обърнете внимание на следното:

Като цяло ясно доказахме, че е необходимо $ \ cos \ ляво (x- \ frac \! \! \ Pi \! \! \ Text< >> \ вдясно) $ беше равно на число, по-голямо от „единица“ и следователно тази конструкция няма корени.

Справяме се с второто:

Ние решаваме тази конструкция:

По принцип можете да оставите отговора така или да го нарисувате:

Важни точки

В заключение бих искал още веднъж да насоча вниманието ви към работата с „грозни“ аргументи, т.е. когато $ \ sin $ и $ \ cos $ не са таблични стойности. Проблемът е, че ако твърдим, че в нашето уравнение $ \ frac $ е $ \ cos $, а $ \ frac $ е $ \ sin $, тогава в крайна сметка, след като решим конструкцията, трябва да вземем предвид и двете от тези изисквания. Получаваме система от две уравнения. Ако не вземем това предвид, ще получим следната ситуация. В този случай ще получим две точки и вместо $ \ varphi $ ще имаме две числа: $ \ arcsin \ frac $ и $ - \ arcsin \ frac $, но последното в никакъв случай не ни устройва. Същото ще се случи и с точката $ \ frac $.

Този проблем възниква само когато става въпрос за „грозни“ аргументи. Когато имаме таблични стойности, няма нищо подобно.

Надявам се днешният урок да ви е помогнал да разберете какъв е методът на спомагателния ъгъл и как да го приложите към примери за различни нива на сложност. Но това не е единственият урок за решаване на проблеми с помощта на спомагателния ъглов метод. Така че останете с нас!