Намиране на двойно свързани компоненти (блокове) на графика

Ако свързаната графика съдържа два върха u1 и u2 такива, че всяка пътека между тях ще премине през върха v, след това отгоре v ще бъде извикан артикулационна точка.

Може да се даде еквивалентна дефиниция на артикулационната точка.

Върх v броя G = извикан артикулационна точка, ако премахването на този връх и всички изходящи от него ръбове води до увеличаване на свързаните компоненти на графиката.

Ако в свързана (състояща се от един свързан компонент) графика няма артикулационни точки, тя е двойно свързана.

Всякакви максимум двойно свързан подграф на графика G Наречен двойно свързан компонентили блок тази графика (фиг. 8.17).

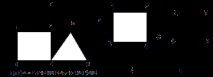
Фигура: 8.17. Блокове на графика G

Въпрос 1. Какво ще бъде пресечната точка на два различни блока на графиката?

Въпрос 2. Какво се случва с блок, ако към него прикачите ръб на графика, който има обща точка с блока и не принадлежи на блока?

Двойно свързаната графика е много полезно свойство за някои приложни проблеми.

Нека си представим, че върховете на графиката са телеграфни станции; ребрата са далекопроводи. Да предположим, че една от станциите не работи. Ако графиката е свързана двойно, тогава останалите две станции ще останат свързани.

За много задачи е важно да знаете блоковете на графиката. Например, намерете всички елементарни цикли на графика G може да бъде отделно за всеки блок на графиката G.

Намирането на артикулационни точки и блокове на графика е класически проблем. Ще търсим артикулационни точки, като обхождаме всички върхове на графиката, като използваме метода за първо търсене в дълбочина. Ние не само ще заобиколим върховете на графиката, но и ще изградим нейния скелет.

Когато се конструира телена рамка с първо търсене на дълбочина за два върха u и v, свързан с ръб, винаги е известен със сигурност: или u - потомък v, или обратно. Как да разпознаем артикулационната точка с, ако рамката вече е изградена д броя G?

Тук критерий за артикулация:

- или това е корен, в който има поне двама сина д;

- или в горната част с има поне един син u такъв, че нито той, нито неговите потомци са свързани чрез акорди с предци с.

Помислете за фиг. 8.18. Числа на върховете - числа, които се получават от върховете на графиката по време на изграждането на каркаса. Нека покажем, че върхът с удовлетворява второто условие на критерия.

Чрез изграждане на рамката с има син 3 и потомък 4. Предшественик с - връх к. Син 3 и неговият потомък 4 не са свързани чрез акорди с к. така, с - артикулационна точка и графика G има първи блок = s–3, 3-4, с–4>.

Фигура: 8.18. Артикулационни точки

Въпрос 3. С кой връх трябва да се свърже връх 4, така че графиката G стана двойно свързан?

Върх к - точката на артикулация, тъй като това е корен, който има двама синове: с и 5. Следователно графиката G има втори блок = и трети блок = .

Познавайки критерия на артикулационната точка, ние описваме алгоритъма за намиране на тези точки.

Нека алгоритъмът за първо търсене в дълбочина изгради каркаса д броя G. За всеки връх v ще изчислим две стойности: GLN[v] и МИН[v].

GLN[v] - само числото, което връхът получава при изграждането на каркаса. Например за корена GLN[к] = 1.

Нека върха v свързани с акорди (не забравяйте какво представляват акордите за рамка д) с някои върхове хедин, ..., хк. Нека да изберем минимума от числата на тези върхове:

Въпрос 4. Кои върхове на графиката на фиг. 8.18, свързани с акорди отгоре с?

Нека бъде w - всеки потомък на върха v. Също така може да бъде свързан чрез акорди с някои върхове. Y.един, ..., Yp.

И накрая, нека преброим Y.[w] за всеки w - потомък v и изберете от тях минимума.

МИН[v] е лесно да се изчисли чрез индукция.

Нека си припомним критерия за точката на артикулация. Това е или корен с двама синове, или предците на тази точка и потомците на поне един син не са свързани с акорди.

Ние пишем този критерий чрез GLN и МИН.

МИН[u] - минималният брой върхове, към които е свързан синът u и неговите потомци. Ако сред тези върхове няма предци v, тогава критерият е изпълнен. Числата на предците са строго по-малко GLN[v], така МИН[u] ³ GLN [v] за някой син u върхове v.

Въпрос 5. Изчисли МИН[3] за син 3 върха с. Ще работи ли с критерий?

Данни: Графика G = без изолирани върхове, представени от инцидентни списъци RECORD [v], v Î V.

Резултати: Наборът от ръбове на всички компоненти на двойно свързани. Променливи МИН, GLN, CTEK, брой - глобален.

1 процедура BLOC (v, p);

Ръбовете на блоковете се избутват върху стека, p е бащата на v>

3 num: = num + 1; GLN [v]: = брой;

5 за u Є RECORD [v] do

6 ако GLN [u] = 0 тогава

8 STACK = GLN [v] тогава

стек последен до (v - u) включително -
блок, свързващ u на всички негови потомци>

14 e p) и (GLN [u] 1) блокове и алгоритъмът работи добре за всяка графика, съдържаща блокове от най-много i-един.

Започваме търсене с дълбочина първо и на някаква стъпка първо срещаме ръб (v - u) такъв, че МИН[u] ³ GLN[v] (критерий). Върх v - корен или артикулационна точка, u - син на върха v. Тъй като критерият беше проверен за първи път, всички потомци u и няма артикулационни точки сред тях. Следователно горната част на стека до ръба (v - u) - първият блок. Нека изтрием този блок, оставяйки само горната част v.

Графиката остава i-1 блока и чрез индуктивната хипотеза те ще бъдат намерени и доказателството е приключило.

Нека изчислим изчислителната сложност на алгоритъма.

Цикъл 2 изисква н върхове ОТНОСНО(н) стъпки. Обадете се БЛОК(v, 0) ще доведе O (n + m) стъпки къде н и м - броят на върховете и ръбовете, тъй като това е необходимото за търсене с дълбочина първо. Всеки ръб в цикъл 13 се отстранява от стека и се отпечатва точно веднъж, т.е. няма повече O (m) стъпки. Сборът от всички тези условия не надвишава O (n + m) стъпки.

Отговор 1. Точка на артикулация или нищо.

Отговор 2. Максимумът на блок означава, че като прикрепяме към него какъвто и да е подграф, ние автоматично прикрепваме точката на артикулация.

Отговор 3. С топ 5.

Отговор 4. Върх 4.

Отговор 5.МИН[3] = 2, тъй като низходящ 3, връх 4 е свързан чрез хорда с с, и GLN[с] = 2. GLN[с] =МИН[3] и критерият е изпълнен.

Пътеки на Ойлер

Ойлер начинв графиката се нарича произволен път, минаващ през всеки ръб точно веднъж.

Ако пътят завършва в началния връх, тогава той се извиква Цикъл на Ойлер(фиг. 8.19).

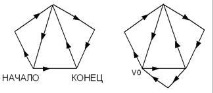
Фигура: 8.19. Ойлеров цикъл, Ойлеров път

Проблемът за съществуването на път на Ойлер в дадена графика е решен от великия руски математик Леонард Ойлер през 1736 г.

Необходимото и достатъчно условие за съществуването на такъв път, който той представи, се счита за първата теорема на теорията на графовете в историята на математиката.

Пътят на Ойлер съществува тогава и само ако графиката е свързана и съдържа най-много два върха с нечетна степен. (Спомнете си, че степента на върха е броят на ребрата, съседни на него).

Имайте предвид, че броят на върховете с нечетна степен във всяка графика е винаги четен. Лесно е да се докаже.

Нека да обобщим градусите на всички върхове на графиката. Тази сума е
2м - два пъти броя на ребрата, тъй като всеки ръб свързва два върха. Приносът към тази сума на върховете с четна степен е четен, следователно приносът на върховете с нечетна степен също трябва да е четен. За да направите това, трябва да има четен брой от тях (нечетен брой ръбове - четен брой върхове = четен резултат).