Методи за решаване на системи с линейни неравенства (стр. 1 от 2)

ФИНАНСОВА АКАДЕМИЯ ПО ПРАВИТЕЛСТВОТО НА РФ

Катедра по математика и финансови приложения

Курсова работа

"Методи за решаване на системи с линейни неравенства"

Изпълнено от студент от група IEC 1-2

Чанкин Петър Алексеевич

Професор Александър Самуилович Солодовников

Графичен метод . 3

Метод с изкуствена основа . 8

Принцип на двойственост . 10

Списък на използваната литература. 12

Определени свойства на системи с линейни неравенства бяха разгледани през първата половина на 19 век във връзка с някои проблеми на аналитичната механика. Систематичното изследване на системите на линейни неравенства започва в самия край на 19 век, но става възможно да се говори за теорията на линейните неравенства едва в края на двадесетте години на 20 век, когато е налице достатъчен брой свързани резултати вече се бяха натрупали.

Сега теорията на крайните системи на линейни неравенства може да се разглежда като клон на линейна алгебра, който е израснал от нея с допълнителното изискване за подреждане на полето на коефициентите.

Линейните неравенства са особено важни за икономистите, тъй като именно с помощта на линейни неравенства човек може да моделира производствените процеси и да намери най-изгодните планове за производство, транспорт, разпределение на ресурси и т.н.

В тази статия ще очертаем основните методи за решаване на линейни неравенства, приложени към конкретни проблеми.

Графичният метод се състои в конструиране на набор от възможни решения на LPP и намиране в този набор на точка, съответстваща на max/min на целевата функция.

Поради ограничените възможности за визуално графично представяне, този метод се използва само за системи с линейни неравенства с две неизвестни и системи, които могат да бъдат сведени до тази форма.

За да демонстрираме визуално графичния метод, ще решим следния проблем:

На първия етап е необходимо да се изгради област от възможни решения. За този пример е най-удобно да изберете X2 като абсциса и X1 като ордината и да запишете неравенствата, както следва:

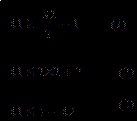
За да намерим граничните точки, решаваме уравненията (1) = (2), (1) = (3) и (2) = (3).

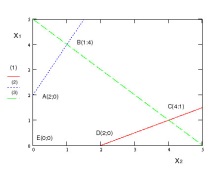
Както се вижда от илюстрацията, многогранникът ABCDE образува областта на възможните решения.

Ако областта на възможните решения не е затворена, тогава или max (f) = + ∞, или min (f) = -∞.

Сега можем директно да намерим максимума на функцията f.

Като заместваме координатите на върховете на многогранника във функцията f и сравняваме стойностите, откриваме, че

f (C) = f (4; 1) = 19 - максимум на функцията.

Този подход е доста полезен за малък брой върхове. Но тази процедура може да се забави, ако има много пикове.

В този случай е по-удобно да се разгледа линия на нивото на формата f = a. С монотонно нарастване на числото a от -∞ до + ∞, правите линии f = a се изместват по нормалния вектор [1]. Ако при такова преместване на линията на нивото има определена точка X - първата обща точка от областта на възможните решения (полиедър ABCDE) и линията на нивото, тогава f (X) е минимумът от f на множеството А Б В Г Д. Ако X е последната точка на пресичане на линията на нивото и множеството ABCDE, тогава f (X) е максимумът от множеството възможни решения. Ако като a → -∞, правата линия f = a пресича множеството възможни решения, тогава min (f) = -∞. Ако това се случи като → + ∞, тогава

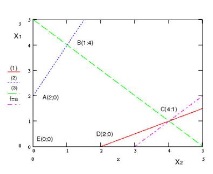
В нашия пример линията f = a пресича областта ABCDE в точката C (4; 1). Тъй като това е последната точка на пресичане, max (f) = f (C) = f (4; 1) = 19.

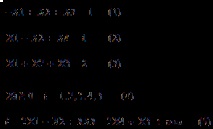
За да започнете да решавате LPP по симплекс метода, е необходимо да доведете LPP до специален формуляр и да попълните симплекс таблицата.

Системата (4) е естествено ограничение и не се вписва в таблицата. Уравнения (1), (2), (3) образуват областта на възможните решения. Изразът (5) е целевата функция. Свободните условия в системата от ограничения и областта на допустимите решения трябва да бъдат неотрицателни.

В този пример X3, X4, X5 са основни неизвестни. Те трябва да бъдат изразени чрез безплатни неизвестни и заменени в целевата функция.

Сега можете да започнете да попълвате симплекс таблицата: