Лекция 21.
Статистическо моделиране
Статистическо моделиране ? основна техника за моделиране, която тества модела с множество случайни сигнали при дадена плътност на вероятността. Целта е да се определят статистически резултатите. Статистическото моделиране се основава на метода на Монте Карло. Спомнете си, че имитацията се използва, когато други методи не могат да бъдат приложени.
Метод на Монте Карло
Нека разгледаме метода на Монте Карло, като използваме примера за изчисляване на интеграла, чиято стойност не може да бъде намерена аналитично.
Цел 1. Намерете стойността на интеграла:
На фиг. 21.1 е графика на функцията е(х). Изчислете стойността на интеграла на тази функция ? след това намерете площта под тази графика.
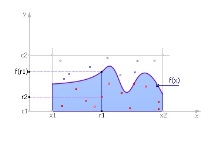
Ограничаваме кривата отгоре, надясно и наляво. Ние разпределяме на случаен принцип точки в правоъгълника за търсене. Нека означим с н1 броят точки, приети за тестване (т.е., попадайки в правоъгълник, тези точки са показани на фиг. 21.1 в червено и синьо), и след н2 ? броя точки под кривата, т.е. тези, които попадат в сенчестата зона под функцията (тези точки са показани на фиг. 21.1 в червено). Тогава е естествено да се приеме, че броят точки, попадащи под кривата по отношение на общия брой точки, е пропорционален на площта под кривата (стойността на интеграла) спрямо площта на тествания правоъгълник. Математически това може да се изрази по следния начин:
Тези аргументи, разбира се, са статистически и толкова по-верни, колкото по-голям е броят на тестовите точки, които вземаме.
Фрагмент от алгоритъма на Монте Карло под формата на блок-схема изглежда както е показано на фиг. 21.2 .
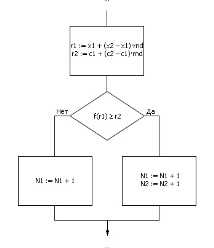
Стойностите r1 и r2 на фиг. 21.2 са равномерно разпределени случайни числа от интервали (хедин; х2) и (° Седин; ° С2) съответно.
Методът на Монте Карло е изключително ефективен, опростен, но е необходим „добър“ генератор на случайни числа. Вторият проблем при прилагането на метода е да се определи размерът на извадката, т.е. броят точки, необходими за осигуряване на решение с дадена точност. Експериментите показват: за да се увеличи точността с 10 пъти, размерът на пробата трябва да се увеличи със 100 пъти; т.е. точността е приблизително пропорционална на квадратния корен от размера на извадката:
Схема на използване на метода на Монте Карло в научните изследвания
системи с произволни параметри
След изграждането на модел на системата със случайни параметри, входни сигнали от генератор на произволни числа (RNG) се подават към нейния вход, както е показано на фиг. 21.3. RNG е проектиран така, че да извежда равномерно разпределени случайни числа rpp от интервала [0; един]. Тъй като някои събития може да са по-вероятни, други ? по-малко вероятно, тогава равномерно разпределените случайни числа от генератора се подават към преобразувател на случайни числа (RNSP), който ги преобразува в зададен от потребителя закон за разпределение на вероятностите, например в нормален или експоненциален закон. Тези преобразувани случайни числа х сервиран на входа на модела. Моделът изработва входния сигнал х по някакъв закон у = φ(х) и получава изходния сигнал у, което също е случайно.
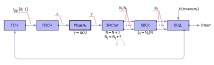
В блока за натрупване на статистика (BNStat) са инсталирани филтри и броячи. Филтърът (някакво булево условие) определя по стойност у, дали някакво събитие е реализирано в конкретен експеримент (условието, е = 1) или не (условието не е изпълнено, е = 0). Ако събитието е реализирано, тогава броячът на събитията се увеличава с един. Ако събитието не се реализира, стойността на брояча не се променя. Ако трябва да наблюдавате няколко различни вида събития, тогава за статистическо моделиране са ви необходими няколко филтъра и броячи. нi . Винаги ли има брояч на броя на експериментите ? н .
Допълнителна връзка нi да се н, изчислено в блока за изчисляване на статистически характеристики (BVSH) по метода на Монте Карло, дава оценка на вероятността стрi възникване на събитие i, тоест показва честотата на появата му в поредица от н експерименти. Това ни позволява да направим заключения относно статистическите свойства на моделирания обект.
Например събитие А се е случило в резултат на 200 експеримента, извършени 50 пъти. Това означава, според метода на Монте Карло, че вероятността от настъпване на събитие е: стрA = 50/200 = 0,25. Вероятността събитието да не се случи е съответно 1 ? 0,25 = 0,75 .
Забележка: когато се говори за експериментална вероятност, тя се нарича честота; думата вероятност се използва, когато искат да подчертаят, че говорим за теоретична концепция.
С голям брой експерименти н честотата на възникване на събитие, получена експериментално, клони към стойността на теоретичната вероятност за настъпване на събитие.
В блока за оценка на надеждността (BOD) се анализира степента на надеждност на статистическите експериментални данни, взети от модела (като се вземе предвид точността на резултата ε, дефиниран от потребителя) и определят необходимия брой статистически тестове. Ако колебанията в стойностите на честотата на възникване на събития спрямо теоретичната вероятност са по-малки от определената точност, тогава експерименталната честота се приема като отговор, в противен случай генерирането на случайни входни влияния продължава и процесът на симулация се повтаря. При малък брой тестове резултатът може да е ненадежден. Но колкото повече тестове, толкова по-точен е отговорът, според теоремата за централната граница.
Имайте предвид, че оценката се базира на най-лошата от честотите. Това осигурява надежден резултат за всички характеристики на модела, който се улавя наведнъж.
Пример 1. Нека решим един прост проблем. Каква е вероятността една монета да падне с главата нагоре, когато тя случайно падне от височина?
Нека започнем да хвърляме монета и да записваме резултатите от всяко хвърляне (вижте таблица 21.1).
Ще изчислим честотата на главите като съотношението между броя случаи на главата до главата към общия брой наблюдения. Погледнете таблицата. 21.1. дела за н = 1, н = 2, н = 3 ? отначало честотните стойности не могат да се нарекат надеждни. Нека се опитаме да изградим графика на зависимост Pо от н ? и нека видим как честотата на заглавието се променя в зависимост от броя на проведените експерименти. Разбира се, при различни експерименти ще се получат различни таблици и следователно различни графики. На фиг. 21.4 показва една от опциите.
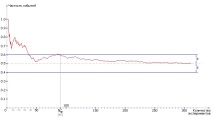
Нека направим някои изводи.
- Вижда се, че при малки стойности н, напр, н = 1, н = 2, н = 3 На отговора изобщо не може да се вярва. например, Po = 0 за н = 1, тоест вероятността да получите глави с едно хвърляне е нула! Въпреки че всички са наясно, че това не е така. Тоест, досега получихме много груб отговор. Вижте обаче графиката: в ход натрупване информация, отговорът бавно, но сигурно се доближава до правилния (подчертава се с пунктирана линия). За щастие, в този конкретен случай знаем верния отговор: в идеалния случай вероятността за получаване на глави е 0,5 (при други, по-сложни проблеми, отговорът, разбира се, няма да ни бъде известен). Да кажем, че трябва да знаем отговора с точност ε = 0,1. Нека нарисуваме две успоредни линии на разстояние 0,1 от верния отговор 0,5 (виж фиг. 21.4). Ширината на получения коридор ще бъде 0,2. След като кривата Pотносно(н) ще влезе в този коридор, така че той никога няма да го напусне, можете да спрете и да видите за каква стойност н случи се. Това е експериментално изчислена критична стойност необходим брой експерименти нcr e, за да се определи отговорът с точност ε = 0,1; ε -кварталът в нашите разсъждения играе ролята на един вид тръба на точността. Имайте предвид, че отговорите Po (91), Po (92) и така нататък не променят много своите стойности (виж фиг. 21.4); поне не променят първата цифра след десетичната запетая, на която трябва да се доверим според условията на задачата.
- Причината за това поведение на кривата е действието централна гранична теорема (вж. Лекция 25 и Лекция 34). Засега тук ще го формулираме в най-простата версия „Сумата от случайни променливи е неслучайна стойност“. Използвахме средното Pоколо, което носи информация за сумата от експерименти и следователно постепенно тази стойност става все по-надеждна.
- Ако направите този експеримент отново от началото, тогава, разбира се, резултатът му ще бъде различен вид случайна крива. И отговорът ще бъде различен, макар и приблизително еднакъв. Нека проведем цяла поредица от такива експерименти (вж. Фиг. 21.5). Такава поредица се нарича ансамбъл от реализации. Какъв е крайният отговор, на който трябва да се вярва? В крайна сметка, въпреки че са близки, те все пак са различни. На практика те действат по различен начин. Първа опция ? изчислява средната стойност на отговорите за няколко реализации (виж таблица 21.2).
- Лекция - Основни елементи на прозореца MS WORD
- Лекция 3
- Лекция 2
- Лекция 13
- Лекция Създаване на валидни XML документи