Директно дискретно преобразуване на Лаплас (страница 1 от 2)

Предмет: Теория на автоматичното управление

Тема: ДИРЕКТНА ДИСКРЕТНА ТРАНСФОРМА НА ЛАПЛАЦИЯ

Динамичните процеси в дискретни системи за управление са описани чрез уравнения в крайни разлики. Удобен метод за решаване на разностни уравнения е оперативният метод, базиран на дискретното преобразуване на Лаплас. Дискретното преобразуване на Лаплас е обобщение на обичайното преобразуване на Лаплас към дискретни функции.

Една от най-важните характеристики на трансформацията на Лаплас е, че много връзки и операции върху оригинали съответстват на по-прости връзки върху техните изображения.

1. Директно дискретно преобразуване на Лаплас

Трансформацията на Лаплас за непрекъснати оригинали е:

Нека получим формули за дискретното преобразуване на Лаплас. За изхода на импулсния елемент можете да напишете съотношението

Замествайки този израз във формулата на Лапласово преобразуване, получаваме

В същото време беше получена една от формулите за дискретно преобразуване на Лаплас, която има вид:

В сравнение с обичайното преобразуване на Лаплас за непрекъснати оригинали, интегралът се заменя със сумата и непрекъснатата променлива -т да дискретни - nT .

Пример 1. Определете дискретното преобразуване на Лаплас за единичната функция х ( t) = 1 ( т).

Решение: Прилагайки дискретна формула на Лапласово преобразуване, получаваме

Ако изображенията на непрекъснати сигнали са уравнения на мощността - f (p n), тогава образите на дискретни функции са експоненциални уравнения - f (e pnT), следователно апаратът на теорията на непрекъснатите системи не може да бъде приложен към тях. Чрез извършване на замяната z = e pT във формула (4) получаваме

Получихме втората формула за дискретното преобразуване на Лаплас, която се нарича z -трансформация. Използвайки z - трансформации, получаваме уравнения на мощността, което ни позволява да прилагаме методи за изучаване на непрекъснати системи за дискретни системи, като се вземат предвид някои характеристики.

Пример 2. Определете дискретно изображение F (z), ако е оригинален f (t) има формата (фиг. 1):

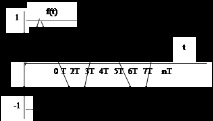
Решение: Функция F (z) може да се представи като поредица

Получи дискретна трансформация на първоначалната непрекъсната функция.

2. Дискретно преобразуване на Лаплас в общ вид

За изхода на импулсния елемент можете да напишете съотношението

За да намерите изображение x * (p) ние използваме теоремата за умножение в сложната област.

Образът на произведението е равен на конволюцията на образите

Въз основа на теоремата за остатъците на Коши, този интеграл може да се определи като сума от остатъци над полюсите на интегранта.

Това е третата формула за директно дискретно преобразуване на Лаплас.

Пример 3. Определете дискретното преобразуване на Лаплас за единичната функция.

Решение: Функции x (t) = 1 (t) съответства на изображението

Записваме характеристичното уравнение и определяме стойностите на полюсите, техния брой и кратност. s = 0, s1 = 0, n = 1, m = 1.

Намерете дискретно изображение, като използвате теоремата за остатъците на Коши на полюсите на интегранта

Пример 4. Определете дискретното преобразуване на Лаплас за линейно нарастващата функция x (t) = t .

Решение: Функции x (t) = t съответства на изображението

Записваме характеристичното уравнение и определяме стойностите на полюсите, техния брой и кратност. s 2 = 0, s1 = 0, n = 1, m =

Намерете дискретно изображение, като използвате теоремата за остатъците на Коши на полюсите на интегранта

Пример 5. Определете дискретното преобразуване на Лаплас за експоненциалната функция x (t) = e - в .

Решение: Функции x (t) = e - в съответства на изображението

Записваме характеристичното уравнение и определяме стойностите на полюсите, техния брой и кратност. с+ a = 0, s1 = - a, n = 1, m = 1 .

Намерете дискретно изображение, като използвате теоремата за остатъците на Коши на полюсите на интегранта

За да намерите дискретни изображения, можете да използвате някоя от горните форми на дискретно преобразуване на Лаплас. Кратка таблица z -трансформациите са дадени в Приложение 3.

3. Модифицирана дискретна трансформация на Лаплас

След времево квантуване на непрекъснатия сигнал на изхода на импулсния елемент, получаваме дискретна функция, съответстваща на решетъчната функция, която представлява стойността на непрекъснатия сигнал в дискретни моменти от времето на работата на импулсния елемент.

Даден непрекъснат сигнал съответства на една решетъчна функция и следователно една дискретна функция. Обратният проблем е двусмислен, т.е. дискретна функция съответства на безкраен набор от непрекъснати функции (фиг. 2а).

За да се получат междинни стойности на решетъчната функция и следователно непрекъснат сигнал, е необходимо IE да се задейства със закъснение (аванс). Размерът на смяната трябва да се промени в рамките на дадена мярка. Ако времето за смяна еeТ, след това 0 £д £ 1.

Ако д = 0 няма промяна, ако д = 1 смяна с 1 часовник.

Посоката на смяната е безразлична, ако се съгласите да се изместите в посока напред. Можете да изместите както решетъчната функция, така и момента, в който IE се задейства. Съгласно теоремата за смяната, промяна в областта на оригиналите съответства на умножение по д ± pT в областта на изображенията.

На диаграмата това може да се посочи както следва (фиг. 2б)