12 Нелокален комплект за бифуркация за елиптична пъпа

В раздел 6 гл. 9, нашите усилия бяха насочени към намиране на точки в деформационното пространство, където съответната функция на има изродени (и следователно нестабилни и водещи до раздвоения) критични точки. Ако функция няма такива точки, тогава нейната форма близо до всяка точка е структурно стабилна и тогава за нея общият брой максимуми, общият брой минимуми и общият брой седла (от които най-често се интересуваме) не се променят при малки смущения. Но функцията може да се окаже глобално нестабилна, без локална дегенерация, поради факта, че при две недегенерирани критични точки приема една и съща стойност.

На фиг. 11.26 (b) показва графика на типова функция с отделни представителни контури. Не е трудно да се провери, че единствените критични точки са недегенерираните седла, тоест стабилни сингулярности. Но произволно малко възмущение може да направи седло, където под друго

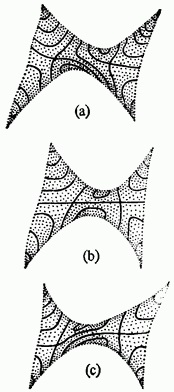
(Фигура 11.26 (а)) или по-висока (Фигура 11.26 (в)). Няма дифеоморфизъм - нито областта на тези функции, нито областта на техните стойности И? - няма да може да съобрази топологичната картина на контури за нито един от тези случаи с картината на фиг. 11.26 (б). Глобалната стабилност на дадена функция изисква не само негенерацията на критичните точки, но и несъвпадението на критичните стойности. Освен това никой дифеоморфизъм, близък до идентичността, не може да комбинира Фиг. 11.26 (а) и (в) (отражение около оста y може, но не може да се запази ориентацията запазваща трансформация). Пътят от (а) до (в) лежи през

Хоризонталните карти на снимки 6 и 7 демонстрират потенциали с нестабилности от този тип, в допълнение към локалната нестабилност, като например дегенеративно сгъване в дясната страна на картата. Съответните снимки на експерименталните потоци показват стабилни съседи на теоретично изчислените потенциали, които не са равностойни в световен мащаб на тях.

За да можем да правим по-подробни прогнози, следователно трябва допълнително да проучим - като част от структурата на бифуркация - набора от онези точки в деформационното пространство, при които критичните стойности съвпадат за съответните функции. Арнолд в [59] нарича този набор слоят Максуел, докато Том, който първи споменава името на Максуел тук, използва термина Максуел набор за случая, когато съвпадението на критичните стойности се извършва в токовете от минимума ( свързвайки го с правилото на Максуел в термодинамиката, което е обсъдено в глава 14). Може би терминът нелокален бифуркационен набор би бил по-подходящ тук (за множеството точки в деформационното пространство, които съответстват на функции със съвпадащи критични стойности), за разлика от локалния бифуркационен набор от тези точки, където съответните функции проявяват локална дегенерация . (Тази терминология има и предимството, че се разпростира и върху по-общия случай на динамични системи, където са възможни много по-интересни нелокални раздвоения, като експлозивната поява на „странни атрактори“ (Chilling-Worth [52]).) Отделни точки, като например точка 4 на фиг. 11.25, могат да принадлежат едновременно на двата бифуркационни множества.

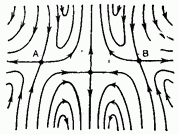
Потокът на фиг. 11.27 не би станал нестабилен като поток, ако функциите на потока имат равни стойности в точки А и Б. Следователно трябва отделно

Фигура: 11.28 (виж сканиране)

дефинирайте множеството седлови връзки за дадена деформация като набор от онези точки в деформационното пространство, за които съответните функции имат критични точки, свързани с някаква линия на нивото. (Ако функциите са дефинирани не на равнината, а в 3, тогава линиите на нивото се заменят с (хипер) повърхности на нивото.) Този набор е, разбира се, подмножество на нелокален бифуркационен набор; в случай на елиптична пъпна и двете групи съвпадат.

На фиг. 11.28 показва карти на нивата на линиите за представителни стойности при фиксирана стойност Лесно е да се види, че пресечната точка на множеството връзки на седлата с тази равнина (равнина на фигурата) се състои от три отворени полулинии, излизащи навън от самото начало, което, както се вижда от фигурата, е точката на сглобяване; следователно пълният (локален, заедно с нелокален) набор от бифуркации изглежда както е показано на фиг. 11.29. Имайте предвид, че преминаването през нелокален набор променя връзките между входящите и изходящите

течения; по-специално се движи единственият „канал“, свързващ противоположни „проливи“ (засенчен на фиг. 11.30).

Следователно експерименталната задача на Бери и Макли беше да се опитат да се "придвижат" доколкото е възможно в границите на нелокален набор от бифуркации. Фактът, че те успяха да останат с толкова голяма точност на това парче повърхност е показател на високата адекватност на тяхната теория.